
Use compass and ruler to construct the following design of a circular
window. How can it be constructed?
What fraction of the area of the circle is in the "triangular "
region in the center bounded by the three arcs?

For the construction it is necessary to see the window in terms of the
circles that make it up, rather than the arcs that are visible. Once we
see the circles in the window the next question becomes what are their relationships
with each other. Then it becomes easier to do the construction. There may
be other, even easier, ways to do this construction, but following are the
steps that I took.
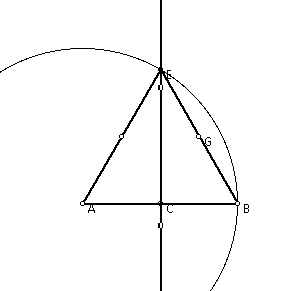
Next, I constructed three circles with centers at A, B, and E. The radii
of each these circles are equal to one-half the the length of a segment
of the triangle.
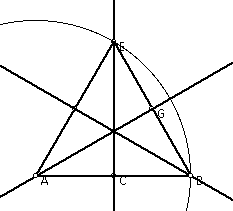
Then it becomes necessary to mark the point of intersection of circle
A with line AG. We do the same for each circle, marking the points of intersection
of the circles with the perpendicular bisector of the segments ( I told
you we would need those perpendicular bisectors). We also marked the point
of intersection of the three perpendicular bisectors. From that point we
will construct a larger circle with center at the intersection of the lines
of bisection and tangent to each circle at the point of intersection of
the circles with the perpendicular bisectors of the triangle's segments.
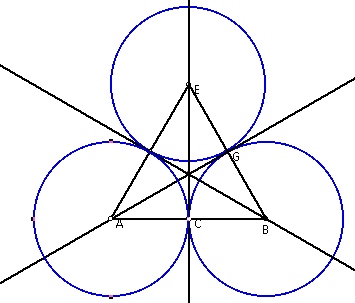
I removed the perpedicular bisectors to keep the picture clean and easy
to work with. Can you see the window in the above figure? If not keep reading!!
The next thing I did was construct an arc on each of the smaller circles.
Each arc went through the midpoints of the segments that the circle intersected
and through the point of intersection between the circle and the perpendicular
bisector and the circle.
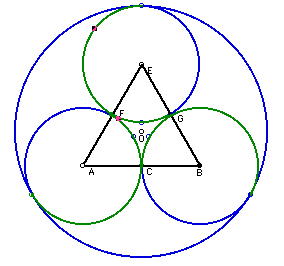
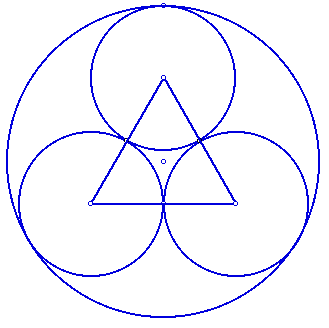
Removal of the blue arcs above yields the following picture. I left the
equilateral triangle in the picture for those who still did not see the
triangle in the original window.
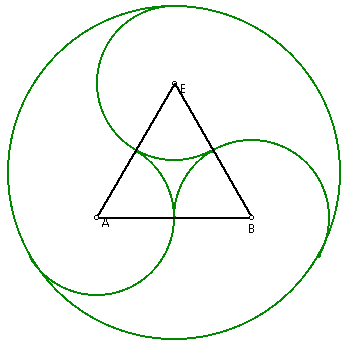
Return to Teisha's Problem Page
Return to Angie's
page
Return to Beth's
Problem Page