
Investigation: Squares on the sides of Parallelograms, Etc.
- On a parallelogram P construct exterior squares on each side.
Prove the centers of these squares form a square.
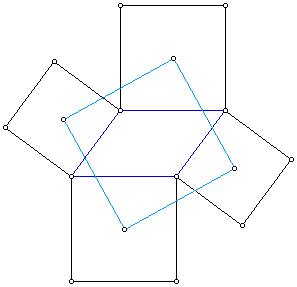
Try some auxillary lines. Suggestion?
- On a parallelogram P construct squares over the interior
on each side. Prove the centers of these squares form a square.
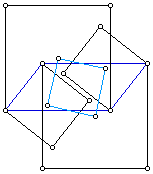
Extension
- Do both of the constructions above on the same parallelogram
and call the area of the square formed by the centers of the
externally constructed squares on the sides to be E, the area
of the square formed by the centers of the squares constructed
to the interior to be I, and the area of the parallelogram to
be P. Use GSP to form a conjecture about these three areas and
then prove your conjecture. Hint.
Extension:
- Generalize the relationship among the areas of the resulting
quadrilaterals when P is an arbitrary quadrilateral. Click here for a GSP sketch (you
may be better off building your own).
- Explore the situation when equilateral triangles are constructed
on each side of the parallelogram P and a resulting quadrilateral
is formed by the centers of the triangles.
- Explore the situation when equilateral triangles are constructed
on each side of the parallelogram P and a resulting quadrilateral
is formed by the vertices of the triangles.
Return to the EMAT
4600/6600 Page.
Reference: Alfinio Flores, Mathematics Monthly,
June-July, 1996, Problem 10533, p. 510.



