

Solution Strategy
 Finding an expression for c in terms
of a and b can ignore the requirement for integer
values. Once we have an expression for (1) we can use it to search
for integer values of a, b, and c.
Finding an expression for c in terms
of a and b can ignore the requirement for integer
values. Once we have an expression for (1) we can use it to search
for integer values of a, b, and c.
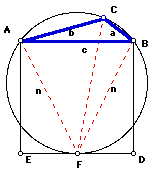
Let the lengths of the sides AF and BF be of length n. Can you solve for n in terms of c?Using the Law of Cosines, from triangle ABC we get
- Note that angle AFC and angle ABC subtend the same chord. Therefore they are equal. Likewise angle BFC and angle BAC subtend the same chord and therefore they are equal. That is, the measure of Angle AFB is the same as the measure of Angle A plus the measure of Angle B. Now, (angle measures) A+B = 180 - C.
- Using the Law of Cosines, from triangle AFB, we get
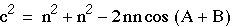
- or
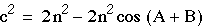
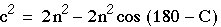
- But angle A + B = 180 - C, so
- From triangle ADF, the Pythagorean relation would give
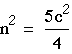
- Therefore
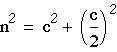
- Substituting in the previous equation gives
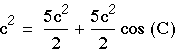
- Divide both sides to get
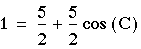
- Substituting in the first Law of Cosines equation from triangle ABC,
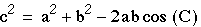
- gives
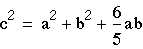
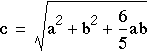
- Thus c is this function of a and b, whether or not the values are integers. The integer values are clear, however, and if (a,b,c ) satisfies the equation, then so does (ka,kb,kc).