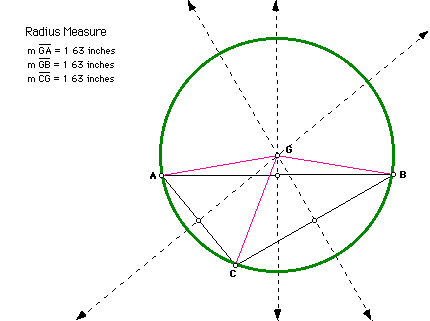

Click here for a GSP script of the above
construction.
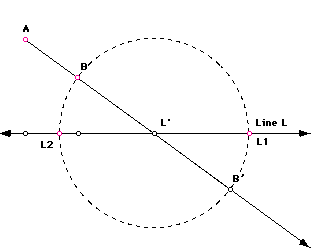
Part 2: Construct a Circle tangent to two points and a line.
Construction: Pick any two points A,B and a line L. Draw a ray from
A thur B intersecting Line L at L' and continuing. Using L' as the center
of a circle and the Segment BL' as the radius, draw a circle. The circle
intersects Line L in two palces, L1 and L2. Choose L2. You now have THREE
points ( A, B, L1 ). Here, repeat the proceedure used in Part 1 above. The
same proceedure could be used with point L1, and you would get a different
circle. Much larger. In face, too large to fit on this screen !
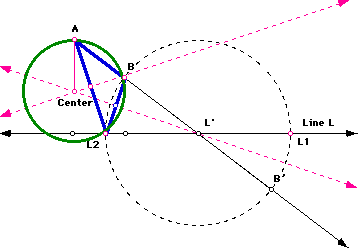
The circle of Apollonius is depicted in green.
Part 3 - 10 of this Problem will be continued during the summer.