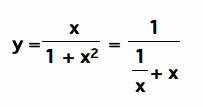
Solution Suggestions with the AM-GM Inequality
Rewrite
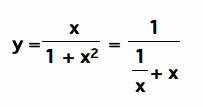
For x > 0, using the arithmetic mean-geometric mean inequality,
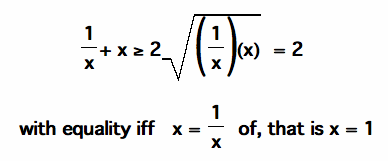
Therefore the value of the function is always less than or equal to .5 and it is equal to .5 only when x = 1.
For x < 0, a similar argument leads to finding the minimum of the function at x = -1. Since the Arithmetic Mean -- Geometric Mean Inequality holds only for postitive values, when x < 0 we have to apply the inequality to - x and - 1/x. We know
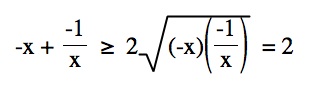
Keep in mind this is for x< 0 so -x and -1/x are postive. Multiplying each side of the inequality by -1 gives
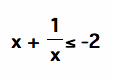
and equality occurs when x = -1. Therefore the value of the function is always more than or equal to -0.5 and it is equal to -0.5 only when x = -1.