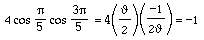(a)
The sublime triangle is an isosceles triangle with base angles
and the angle opposite the
base is. Let triangle ABC be a sublime triangle with base BC, and construct the angle bisector of angle C produced to its intersection with AB at D. Let DB = b and BC = a.
Then triangle CDB is similar to triangle ABC and CD = a, AD = a, AB = a + b, AC = a + b. The similarity allows the equation
and the ratio a/b is the golden ratio
the solution to the equations
or
.
(b) Angle DCB is
and using the law of cosines we can write
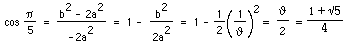
Angle CDA is
and using the law of cosines we get
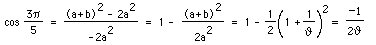
Therefore