Click Here to get the Excel file for this activity

Problem Statement:

Our class was to investigate the logistic function through an in class simulation of the spread of a disease.

Description:
Our in class activity began by assigning each student in the class a number, while giving each student a die and a data sheet. Then, to stimulate the transmission of diseases, we were to find a partner, shake hands with that partner, write down their identification number, and roll the dice. The activity consists of five stages, each lasting 2 minutes. If the sum of our dice was 5 or less, this was considered a risky encounter. If the sum of the dice was greater than five, the encounter was safe. After each encounter, we were to record the identification number of our partner and whether the encounter was risky.

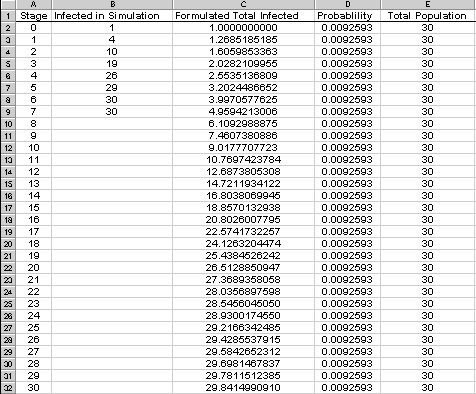
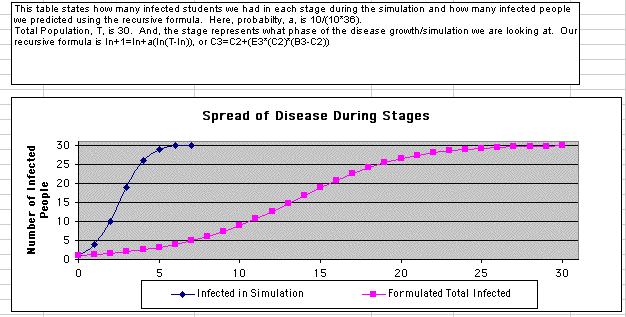
At the end of the five stages, we recorded how many students were infected during each stage of the activity, and we graphed these data points on a graph titled "Spread of Disease." Finally, on the second day of this investigation, we explored how to develop a recursive formula that can more easily help us find the number of infected students during each stage. During this class period and the following class period, we developed the formula In=In+(10/36)*(1/30)*In*(T-In). The explanation of this formula follows later in the write up.

Data Sheet (including graphs)

Please see attached.

Development of Recursive Formula:

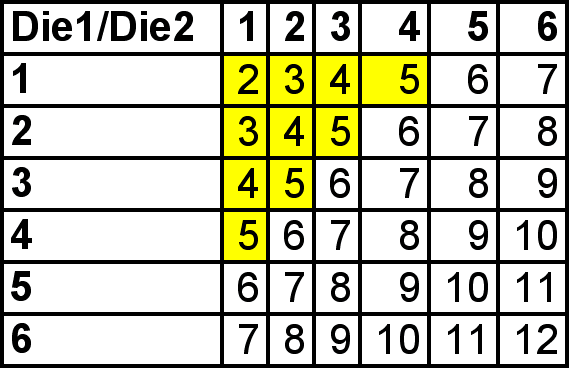
The recursive formula that we developed in class was In+1=In+(10/36)*(1/T)*In(T-In). This formula could help us determine how many predicted infected students there would during a given stage n. In represents the number of infected people from the previous stage. (10/36) represents the probably of an encounter being risky. The follow table illustrates the total number of sum possibilities of two random dice being thrown. The highlighted numbers represent the risky encounters.

Note that there are 10 risky encounters out of a total of 36 possible dice sums. Thus, the probably of a risky encounter is represented by (10/36). Next, we must use a constant that is a fraction in order to restrict the number of people infected. Here, we used the convenient constant 1/30 or (1/T). T represents the total number of participants in the simulation. Thus, (T-In) represents the total number of people in the simulation minus the number of infected people during the previous stage. This tells us how many people are not infected. Thus, In*(T-In) represents the number of people not infected times the number of people who are infected. This excludes the possibilities of an encounter with two infected people or two non infected people. Obviously, if and infected person shook the hand of an infected person, they would still be infected. Also, if a non-infected person shook the hand of a non-infected person, the encounter would always be a safe encounter. Therefore, In(T-In) excludes the circumstances where there is an encounter between two healthy people, and two people who were infected at least one time before the encounter. Overall, this formula In+1=In+(10/36)*(1/T)*(In*(T-In)) helps us to predict how many people would be infected during a given stage n.

Appendix A: Spreadsheet with Collected data and data generated by recursive formula

Click Here to get the Excel file for this activity

Appendix B:

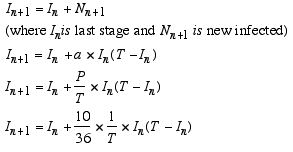
P= The probability to have the risky number = 10/36

(11, 12, 13, 14, 21, 22, 23, 31, 32, 41)

T = Total number of people