Proof of Alternate Interior Angles

by Michelle Corey, University of Georgia

and Kristina Dunbar, Russell Kennedy, Floyd Rinehart, UGA

Alternate Interior Angles:

Suppose that L, M, and T are distinct lines.  Then L and M are parallel if and only if alternate interior angles of the intersection of L and T and M and T are equal.

Proof:

=>    Assume L and M are parallel and prove that alternate interior angles are congruent.

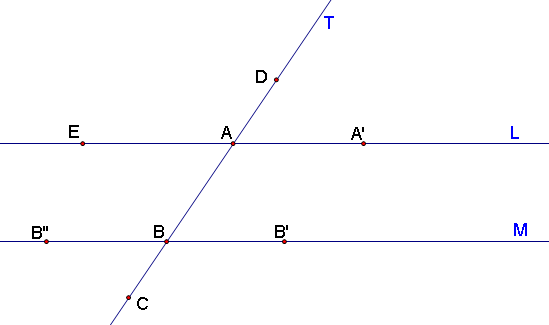
We are given distinct lines L, M, and T.  Assume that L and M are parallel.  By the definition of a line, we can create points D on line T and E on line L, as shown above.  Since angles are determined by two rays (by the angle axiom), angles DAB, DAA', EAA', and EAB exist. 

We want to show that angle A'AB is congruent to ABB'' and that angle ABB' is congruent to BAE.  Since L and M are parallel, by the corresponding angles theorem, DAA' is congruent to angle ABB'.  Because point A lies on the line between points D and B (straight angle theorem), angle DAB is a straight angle and measures 180º by definition of a straight angle. 

By the angle axiom, DAA' + A'AB = DAB = 180º.  Similarly, B''BB' is a straight angle measuring 180º.  ABB' + ABB'' = B''BB' = 180º.  Using algebra, we see that A'AB = 180º - DAA' = ABB''.  By the transitivity property of equality, alternate interior angles A'AB and ABB'' are congruent.

We still need to show that ABB' is congruent to BAE.  Angle EAA', by the straight angle theorem, is a straight angle and measures 180º.  By the angle addition axiom, A'AB + BAE = EAA' = 180º.  Then BAE = 180º - A'AB.  We know from angle addition and corresponding angles that A'AB = 180º - DAA', and that DAA' = ABB'.  So by substitution, EAB = ABB'.  Therefore, alternate interior angles of parallel lines crossed by a transversal are congruent.

<=    Assume alternate interior angles of the intersections of L and T, M and T are congruent and prove L and M are parallel.

We are given lines L, M, and T.  Assume that the alternate interior angles are congruent, i.e. that EAB = ABB' and A'AB = ABB''.  We need to show that L and M are parallel. 

By the straight angle theorem and the angle addition axiom, A'AB + EAB = 180º.  Likewise, B'BA + ABB'' = 180º.  By substitution, A'AB + ABB' = 180º and EAB + ABB'' = 180º.  Since the interior angles on the same side of the transversale are supplementary, L and M are parallel.

We can also prove that L and M are parallel using the corresponding angles theorem.  By angle addition and the straight angle theorem, DAA' + A'AB = DAB = 180º.  Then, using algebra, DAA' = 180 - A'AB = EAB.  By transitivity of equality, DAA' = EAB.  Since EAB = ABB', DAA' = ABB'.  By the same process, I can show that the other sets of corresponding angles are also congruent, i.e. that TAE = ABB'', A'AB = B'BC, and that EAB = B''BC.  Hence, since all sets of corresponding angles are congruent, lines L and M are parallel.

|| Parallels Main Page || Kristina Dunbar's Main Page || Dr. McCrory's Geometry Page ||