Proof of Corresponding Angles

by Floyd Rinehart, University of Georgia

and Michelle Corey, Kristina Dunbar, Russell Kennedy, UGA

Corresponding Angles:

Suppose that L, M and T are distinct lines.  Then L and M are parallel if and only if corresponding angles of the intersection of L and T, and M and T are equal.

Proof:

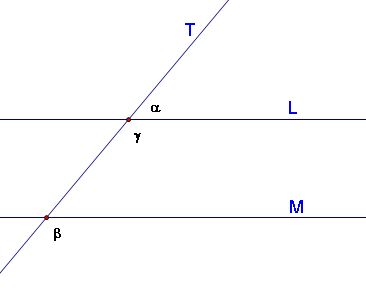
=>  Assume L and M are parallel, prove corresponding angles are equal.

Assuming L||M, let's label a pair of corresponding angles α and β.  We know that angle γ is supplementary to angle α from the straight angle theorem (because T is a line, and any point on T can be considered a straight angle between two points on either side of the point in question).  Note that β and γ are also supplementary, since they form interior angles of parallel lines on the same side of the transversal T (from Same Side Interior Angles Theorem). 

Therefore, since γ = 180 - α = 180 - β, we know that α = β.  This can be proven for every pair of corresponding angles in the same way as outlined above.

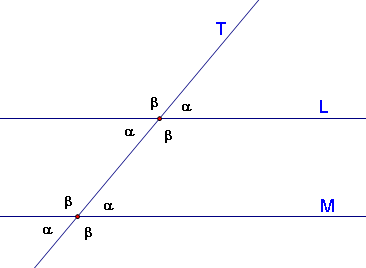
<=  Assume corresponding angles are equal and prove L and M are parallel.

Assuming corresponding angles, let's label each angle α and β appropriately.  By the straight angle theorem, we can label every corresponding angle either α or β. 

For example, we know α + β = 180º on the right side of the intersection of L and T, since it forms a straight angle on T.  Consequently, we can label the angles on the left side of the intersection of L and T α or β since they form straight angles on L.

Since, as we have stated before, α + β = 180º, we know that the interior angles on either side of T add up to 180º.  By the same side interior angles theorem, this makes L || M.

|| Parallels Main Page || Kristina Dunbar's Main Page || Dr. McCrory's Geometry Page ||