Proof of Same Side Interior Angles

by Kristina Dunbar, University of Georgia

and Michelle Corey, Russell Kennedy, Floyd Rinehart, UGA

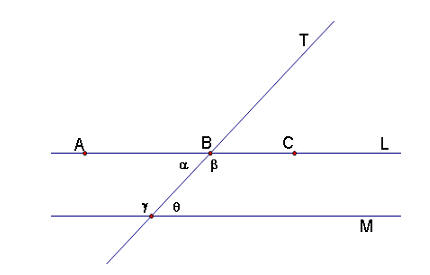
Same Side Interior Angles:

Suppose that L, M, and T are distinct lines.  Then L and M are parallel if and only if same side interior angles of the intersection of L and T and M and T are supplementary.

Proof:

=>  Assume L||M and prove same side interior angles are supplementary.

Assume L||M and the above angle assignments.  Then α = θ and β = γ by the alternate interior angle theorem. 

We know that A, B, and C are collinear and B is between A and C by construction, because A and C are two points on the parallel line L on opposite sides of the transversal T, and B is the intersection of L and T.  So, angle ABC is a straight angle, or 180º.

So, we know α + β = 180º and we can substitute θ for α to get θ + β = 180º.  So, these two same side interior angles are supplementary.

Now, substitute γ for β to get α + γ = 180º. 

We have now shown that both same side interior angle pairs are supplementary.

<=  Assume same side interior angles are supplementary, prove L and M are parallel.

Assume the same side interior angles of L and T and M and T are supplementary, namely α + γ = 180º and θ + β = 180º.  Then, by the parallel axiom, L and M do not intersect because the interior angles on each side of the transversal equal  180º, which, of course, is not less than 180º.  So, because they do not intersect on either side (both sides' interior angles add up to 180º), than have no points in common, so they are parallel.

Addendum:

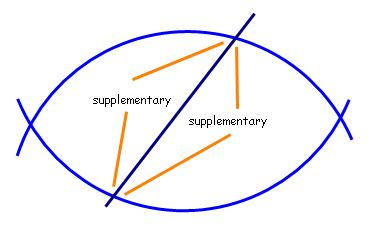
Illustration:  If we know that θ + β = α + γ = 180º, then we know that there can exist only two possibilities:  either the lines do not intersect at all (and hence are parallel), or they intersect on both sides.  However, lines L and M could not intersect in two places and still be distinct.  This would be impossible, since two points determine a line.  Therefore, L||M.

|| Parallels Main Page || Kristina Dunbar's Main Page || Dr. McCrory's Geometry Page ||