By Soo Jin Lee and Jaehong Shin

Primary Learning Outcomes

Increase students' appreciation of whatrepresents and help them arrive at their own approximations of within bounded limits.

Grade : 9-12

Objective : Preparation for the idea of limit and continuity in precalculus context

Procedures/Activities

The purpose of following activities is to help student's appreciation ofby demonstrating that the circumference of a circle can be approximated by considering the inscription and circumscription of a series of approximated by considering the inscription and circumscription of a series polygons.

Activities 1 : Triangle and Circle

Description :

By using GSP, make students to draw a circle given a raius.

and make students to draw a inscription triangle and circription triangle of the cirle.

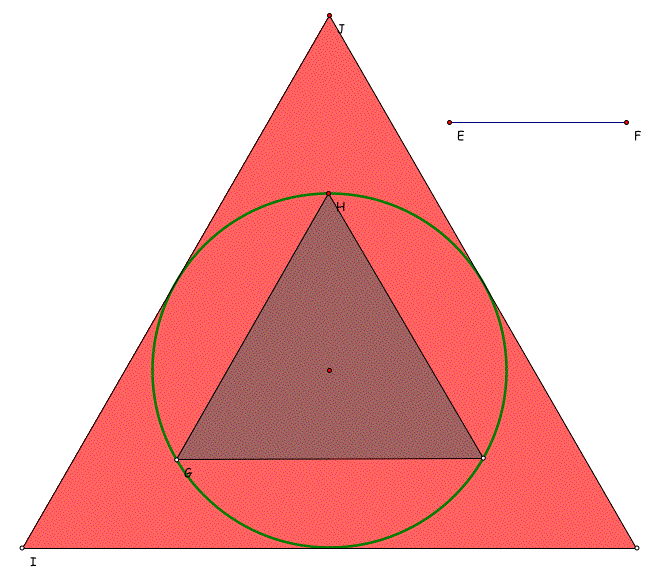
Students should realize that the lengh of the circumference of the circle will be somewhere between the length of the two perimeters. i.e. from the figure, students should guess the perimeter of the circumscribed triangle will longer than the circumference of the interior circle and the perimeter of the inscribed triangle will less than the circumference of the circle in length.

Now, calculate the ratio R between the perimeter of circumscribed circle and diameter of the circle and between that of inscribed circle and diameter of the circle. : triangle.gsp

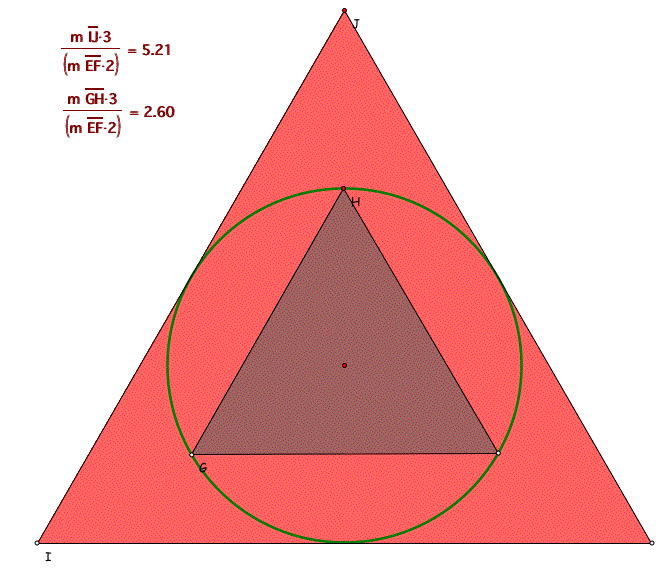
Activitiy 2 : Hexagon and Circle

Like the case of activity 1, make students to draw a circumscribed and inscribed hexagons of the circle and calculate the ratio R. : Hexagog.gsp

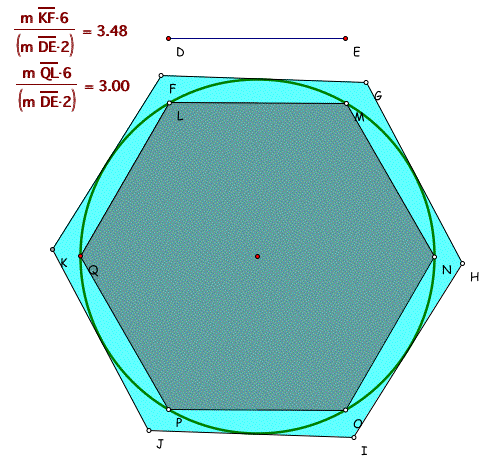
Students should have no problems in seeing that the perimeter lengths of the circumscribed and inscribed hexagons are shorter and longer respectively than those of the preceeding triangles. That is, the comparison of perimeter length among those is following.

Activity 3 : Octogon and Circle

Again, make students to draw a circumscribed and inscribed octogons of the circle and calculate the ratio R. : Octogon.gsp

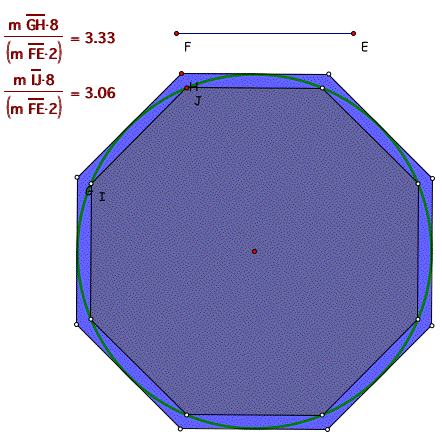
Basically, this is where we modify the approach taken by Archimedes, Through reapeating above processes students can guess the ratio of perimeter lengths of circumscribed and inscribed polygons to the length of converge to one value, that is,, as the number of faces increase.

At elementary levels, just showing above demonstrations can help students appreciateas value in a bounded limit, not as only a constant. In addition, students become to gasp a rough idea of 'limit or 'infinity' , which could be a good prerequite for studying the notion of 'limit' at high school levels.

Extension for Secondary Levels :

Now, if students already knew the notion of trigonometric ratios in secondary levels, they can learn the notion ofas a limit using the basic trigonomtric function keys on a calculator.

First, start by calculating the lengths of one side of a hexagon. Students should begin by constructing two circles of the same arbitrary radius which can be set to r = 1. By using a GSP, hexagons can be readily constructed in the following fashion.

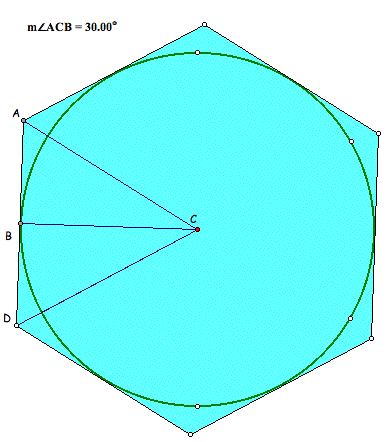
Explore by using GSP. Hexagon1, Hexagon 2.

Students might first consider the circumsrcibed hexagon in the first figure. By drawing a line from the centre C to the vertex A and another from C to the mid-point of AD which is labelled B, it should be clear that triangle ABC is right-angled. It should also be clear that angle ACB is 30 degrees. Now, students can see that if we can find AB, we have found the length of half the side of a hexagon.

They should be able to work out that:

tan(60/2) = tan(30) = AB / 1
AB = tan(60/2)
perimeter of circumscribed hexagon = 2 x 6 x tan(60/2)
< 12 tan(60/2)/2
< 3(2) tan(60/2)

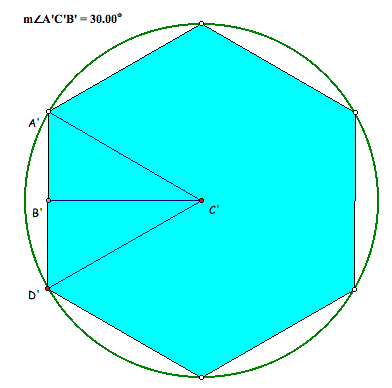
The class should then draw the diagram shown in second one above to consider the case of the inscribed polygon. In a way similar to that just shown, students should see that the half-length of a side to the hexagon is AB, and so:

  sin(60/2) = sin(30) = AB / 1
AB = sin(60/2)
perimeter of inscribed hexagon = 2 x 6 x sin(60/2)
> 12 sin(60/2)/2
> 3(2) sin(60/2)

So now we have a bounded limit for

3(2) sin(60/2) << 3(2) tan(60/2).

Now we want to double the number of sides to the polygons so that we get a better approximation of the circumference. Students should quickly grasp that this is done by bisecting the angle ACB in each case as following.

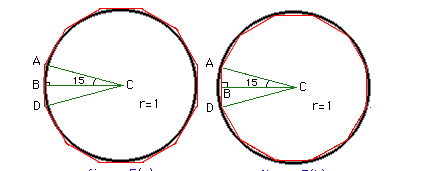
It is easy to show that by following the steps for the case of the hexagon, we can get

For example for the circumscribed polygon

Incidentally, does this process suggest that a circle is a polygon with an infinite number of sides?

Sequences

By now it may have occurred to some students, at least those who have some knowledge of sequences and series, that two sequences emerge from the continuous doubling of the number of the sides and the bisection of the angles. The number of sides of the polygons are

6 = 3(2), 12 = 3(2x2), 24 = 3(2x2x2), 48 = 3(2x2x2x2),...

and the angles are

30 = 60/2, 15 = 60/(2x2), 7.5 = 60/(2x2x2), 3.75 = 60/(2x2x2x2),...

Thus, we can state that

With this limit-bounded formula, students could of course play around with their calculators to get various approximations of . If your class has access to a standard spreadsheet, you may wish to try the following activity.

Using Computers

It is simple enough to use a standard spreadsheet to get a table of successive approximations of .

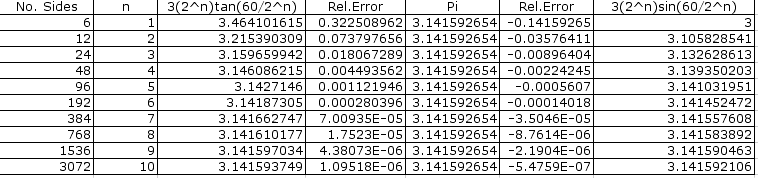
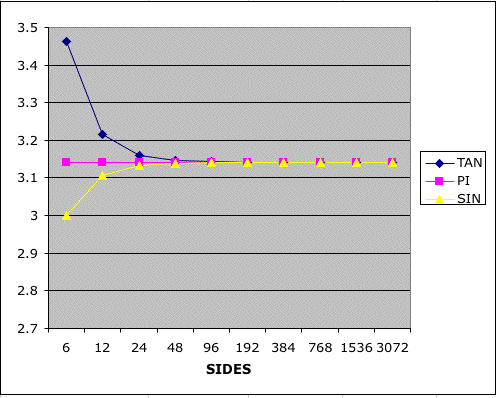
At this point, students could reflect on:

which side of the limit, 'tan' or 'sin' boundaries, starts-off as a better approximation to the rates at which they appear to converge towards. Plotting the data might assist:

Exploration : ApproximationOfPi.xls

Return