Using Graphing Calculator 3.2, we are able to explore the results of:
This second degree equation can be shown when a = 1 as:
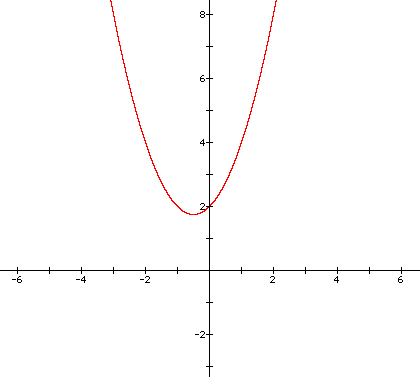
for intersections of all graphs?
Because of the + 2 on this end of this equation, our parabola will always intersect the y-axis at y=2. No matter what value is chosen for a, we can see when x=0, y=2. Therefore, in our exploration of this equation we can expect that all of our parabolas generated will produce graphs that intersect at the common point (0,2). To see the basic algebra steps, click here.
when a = 0?
We can anticipate what the graph would like like when a=0. Using basic algebra skills, when a=0, our resulting equation is no longer of the second degree. This means, our resulting equation will not be a parabola, but will instead be a line with the equation y=x+2. To see the basic algebra steps, click here. While exploring this equation we can already see a line will be generated instead of a parabola, only when the equation is no longer of the second degree, or when a=0.
when a > 0?
The parabola generated when a is a positive value will open upward. This means all corresponding y values on the parabola will be greater than the y value expressed at the vertex. For a diagrammatic explanation of positive a values, click here.
when a < 0?
The parabola generated when a is a negative value will open downward. This means all corresponding y values on the parabola will be less than the y value expressed at the vertex. For a diagrammatic explanation of negative a values, click here.
Testing our expectations, we can graph the following equations for varying values of the coefficient a:
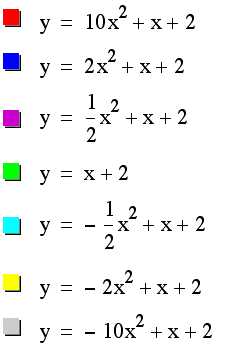
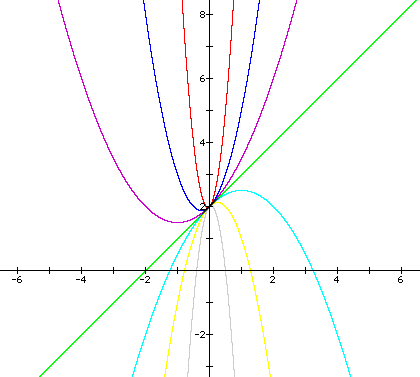
As a approaches zero the corresponding parabola widens, and gets closer to the straight line when a = 0. As a gets larger, the corresponding parabola becomes more narrow as shown above. What do you think the graph would look like if the value of a = 1/100? What about a = 100?
View the animation of our parabola as the value of a goes from -10 to 10.