
The problem: Construct a square having area equal to a given circle.
While this may seem like a relatively simple problem, one quickly discovers that a solution can be quite ellusive. In fact, this problem is one of three famous problems that can not be solve using Euclidean tools, that is a compass and straightedge. This fact makes employing the quadratrix curve most useful.
To get started on this problem, we will rely on some algebra to provide information about the square we are trying to construct. The problem begins with a given circle. Thus we will start with the circle below, with an assumed radius of 1.

And so we are trying to construct a square
with area pi, that is one with side length of ![]() .
.
While constructing segments with irrational
length, such as the square roots of integers, is relatively simple,
constructing a lenght of ![]() is more challenging.
is more challenging.
Recall that the x-intercept of our quadratrix curve was -2/pi. Using this curve we can construct a segment of length 2/pi (segment ON in the figure below) which we will use as our starting point.



Now, we are equipt with a segment having length 2/pi and a segment having length 1 (the radius of the circle and also segment AO of our quadratrix).
Next we'll bisect segment NO to generate a segment (PO) of length 1/pi.
The next goal is to form similar right triangles. To do so, we'll need a right triangle with hypotenuse 1+1/pi. After forming a segment with length 1:1/pi, one must simply construct a semicircle having that segment as its diameter to generate a set of right triangle candidates. Check it out below.

In particular, we are interested in the right triangle in which T lies on the line through U perpendicular to RS (shown below).

In this figure, triangles RUT, TUS, and RTS are similar. Thus the following is true:
Not quite what we're looking for, but very close. In fact, the only step left is to find the segment whose length is the reciprocal of TU (the lenght of that segment will, of course, be the square root of pi).
To do this we'll again rely on similar right triangles.
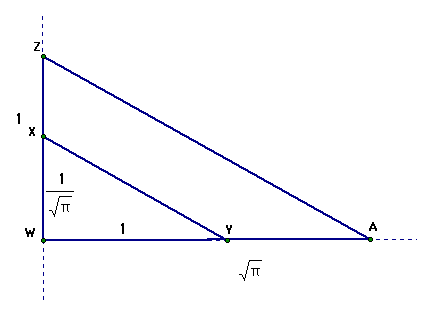
In this figure segments ZA and XY are parallel. Consequently, triangles XWY and ZWA are similar and the following is true:

Ah hah! We have a segment with length square root of pi. Now we simply need to use segment WA to construct our square. Check it out below.

Look familiar . . . ?