The Problem: Trisect an Angle

While the statement of this problem is absurdly simple, finding a solution has proven challenging (impossible?). Any high school geometry student is familiar with the procedure to bisect an angle. However, dividing an angle into three congruent pieces is another matter . . .

One solution is proposed through the use of the Quadratrix Curve [insert history of the quadratrix].

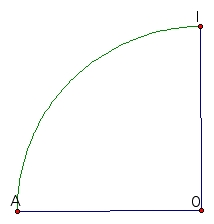
The Quadratrix is built within a circle (or quarter of a circle) much like the one shown below.

The idea is to move a ray through O from point I to point A and simultaneously move a line perpendicular to IO from point I to point O. These two lines will each move at a constant rate complete their travel at precisely the same moment (i.e. the ray reaches point A when the perpendicular line reaches point O).

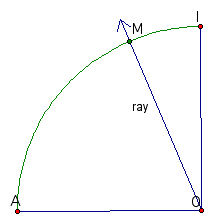
Accomplishing this task relies on determining how fast the ray and line must move in relation to one another.

Selecting a rate of movement for the line is a relatively simple task - we can simply choose any value of linear motion (e.g. 3cm/s).

However, the rate of movement of the ray can be considered in either of the following two ways: (1) how many radians are swept out per unit time (e.g. 2 radians/s) or (2) what the linear distance that a point on the circumference of the circle traveled in a unit of time (e.g. 1.5cm/s)

In using Geometer's Sketchpad softward to create our curve, it proves easiest to consider the motion of the ray as a linear distance per unit time.

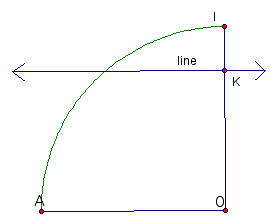
It turns out that what we want is for point K (where the line intersects the radius of the circle) to move a distance equal to the radius in the same amount of time that it takes for point M to move 1/4(2r).

So, what is the ratio of rate for the movement of these two points? Check it out below.

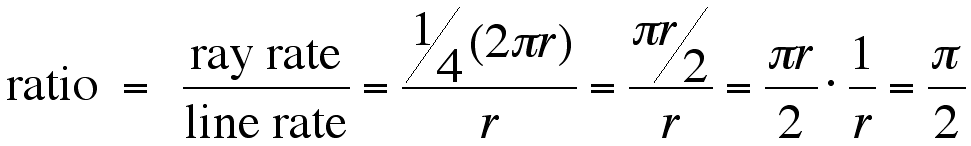
Therefore for a given rate 'a' of the movement of the line, the rate of the movement of the point M must be

In this Geometer's Sketchpad file, the movement of the line and the movement of M have been set to have a ratio of .

The curve is created by the intersection point of the ray and the line (point C on the figure below).

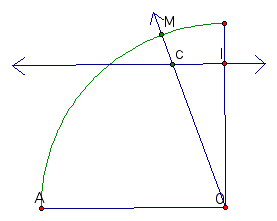
A trace of the intersection point yields the following curve:

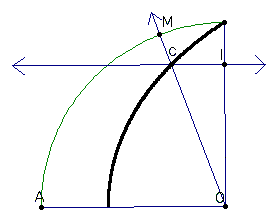
And this curve is lovingly referred to as the quadratrix!

Essentially, this curve serves to correlate linear distance to angular distance.

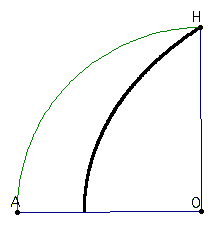
For example, the bisector of angle AOI can be found by constructing the midpoint of segment OH. The point where the line perpendicular to HO passing through this midpoint intersects with the curve lies on the angle bisector. Why? By construction, we know that when the line (see previous diagrams) has travelled halfway down the radius, the ray has moved halfway around the arc (and consequently swept out half of the the total measure of angle AOH).

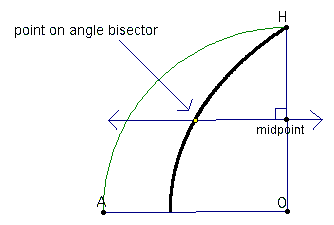
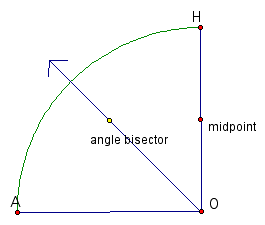
Trisecting the angle is accomplished by trisecting the line segment OH! Check it out below.

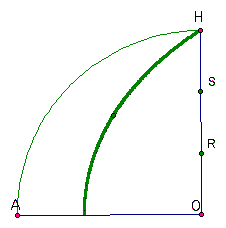
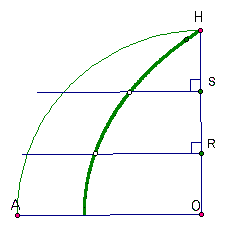
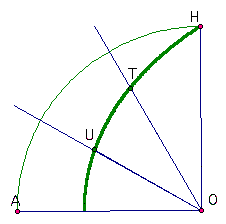
By construction, the ray swept out the area of the sector in the time it took for the point to move the length of the radius. Correspondingly, when the point had moved 1/3 of the length of segement OH, the ray must have swept out 1/3 of the sector (or 1/3 of the 90 degree angle). While this may not be impressive given the fact that one can easily construct a 60 degree angle which can be bisected to form a 30 degree angle, an explanation of how this curve can be used to trisect any angle can be found here.

Also, you can click here to take a look at an algebraic representation of the quadratrix.

An application of the quadratrix is the problem of Squaring a Circle. Find out more about that here.