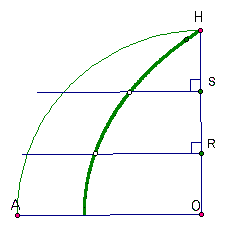

While creating and representing the quadrix proved to be an interesting task, the true utility of this curve lies in its ability to help trisect angles (something not possible using simply the compass and straightedge). Let's take a look at how to accomplish this.
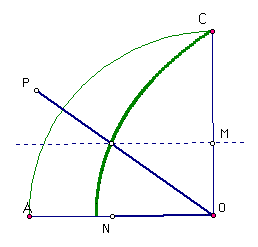
By trisecting the radius of our circle, we were able to use the quadratrix to trisect the associated 90 degree angle as shown below



Utilizing the quadratrix curve to trisect any angle is accomplished in a very similar manner. The trick is to align one side of the angle to be bisected with the base of the quadratrix (segment AO in our diagram). Here's an example.

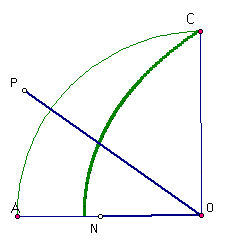
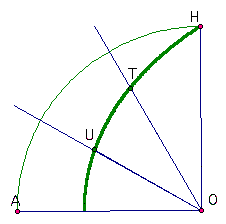
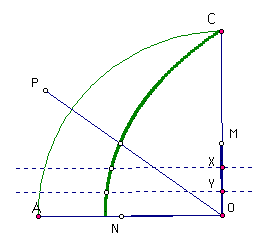
Once the angle is lined up with the quadratrix, one must locate the intersection of the curve and the second leg of the angle. By constructing a perpendicular throught that point, one can easily mark a point , M, at that height on the radius CO. The MO becomes the segment that we must trisect. In doing so, we find the points X and Y along CO.


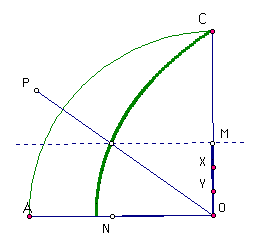
By constructing perpendicular lines to CO through X and Y, we can locate the points on the quadratrix curve through which the angle "trisectors" must pass. One must simply connect those intersection points to the vertex of the angle to complete the trisection. Check it out below.


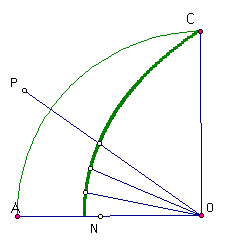
The ability to bisect angles, combined with the ability to perform angle trisection means that any angle can be divided in half or in third. By combining these procedures, an angle can be divided may ways, including into fourths, sixths, and twelfths.
One question that remains to be answered is what integer valued angles can now be constructed with our bisection and trisection tools. To answer this question, one must consider iterations of bisection and trisection.
In particular, any possible integer-valued angle would be created by conducting a a series of bisection and trisections on a 360 degree angle. The resulting degree measure could be represented as follows:
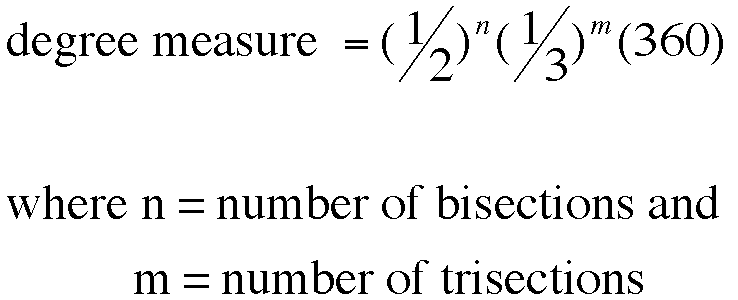
The following table offers a glimpse of different degree measure that can be created through bisection and trisection:
| m\n | 0 | 1 | 2 | 3 | 4 | 5 |
| 0 | 360 | 180 | 90 | 45 | 22.5 | 11.25 |
| 1 | 120 | 60 | 30 | 15 | 7.5 | 3.75 |
| 2 | 40 | 20 | 10 | 5 | 2.5 | 1.25 |
| 3 | 13.3333333333333 | 6.66666666666667 |
|
1.66666666666667 | 0.833333333333333 | 0.416666666666667 |
| 4 | 4.44444444444444 | 2.22222222222222 | 1.11111111111111 | 0.555555555555556 | 0.277777777777778 | 0.138888888888889 |
| 5 | 1.48148148148148 | 0.740740740740741 | 0.37037037037037 | 0.185185185185185 | 0.0925925925925926 | 0.0462962962962963 |
We see that angles with integer measure occur with 2 or fewer trisections and 3 or fewer bisections. This table shows that angles with the following integer measures are possible to construct:
Now a question - is it possible to add or subtract any of these 12 angle measures to create other angles? Notice that the smallest integer angle listed has a measure of 5 degrees. Certainly it is possible to add multiple 5 degree angles together to form new angles. Consequently, we can form angles having any measure equal to a multiple of 5. These angles are shown in the chart below.
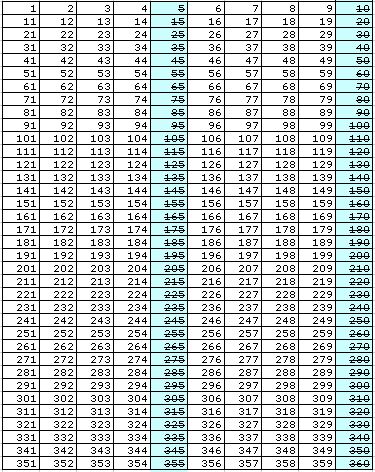
Thus far, we've only found about 1/5 of the total number of angles with integer measure can be created through bisection and trisection. Are there more? Perhaps we can add or subtract some of these angles (shown in blue) to find more angles . . .
Notice that every possible angle is a multiple of 5. What would happen if we added or subtracted combinations of these angles. In general we could imagine adding 5g to 5f, where 5g and 5f represent one of the possible angles. Note f and g must be positive integer values less than 72 (that is, 360/5). Through adding or subtracting we find the following occurs:
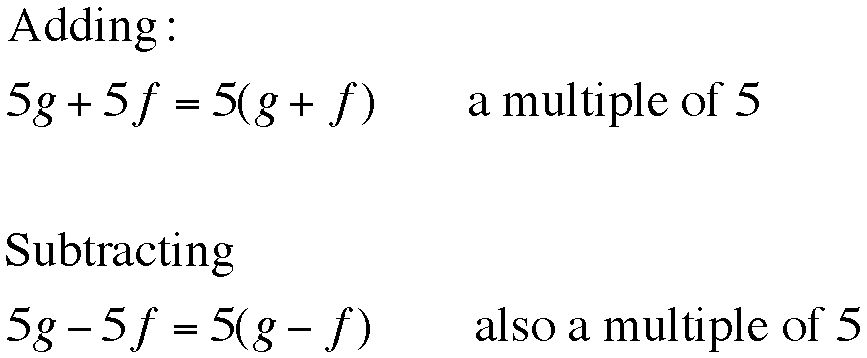
And so addition or subtraction of possible angles always yields a multiple of 5. Since we have already included all multiples of 5 that are less than or equal to 360, no new angles are formed.
So it seems that with bisection and trisection
we are equipt to create about 1/5 of the total number of angles
having integer measure.