EMAT 6680 Assignment 3

Quadratic and Cubic Equations

By Victor L. Brunaud-Vega

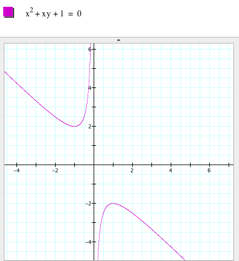
Let us try the equation x² + bx +1 =0

In order to graph the equation using the software Graphing Calculator, we must replace b and use y. Here is the graph where x=y=1.

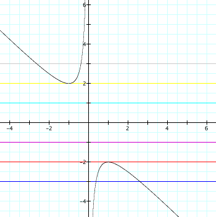
If we give a different value to y, we are adding a line to the graph, parallel to the x axis, and possibly intercepting the curves. The picture shows graphs for different values of y, in this case -3, -2, -1, 0, 1, 2, and 3.

If the line intersects the curve in the xb plane, the intersection points correspond to the roots of the original equation for that value of b.

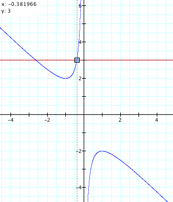
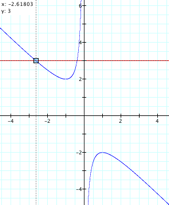
For each value of y we get a horizontal line. In the graph, for b=y=3, we get two negative real roots of the original equation:

x=-0.381966 and x= -2.61803

Another observation is that there is no roots when the value of b=y is between 2 and -2.

Now, if we change the value of c=1 to c=-1, the graph includes a new set of parabolas, as you can see in the picture below.

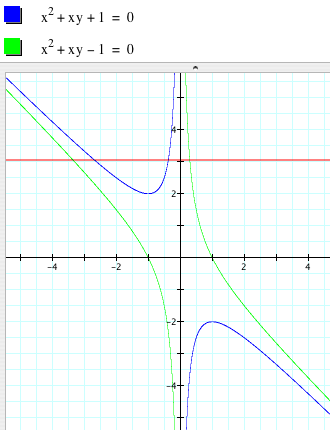
So, what happens if we try different values for c?

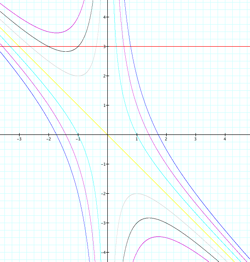
When the value of c=0, the curve becomes a straight line and crosses the origin of the system (0,0).

Now, what happens if 2x + b = 0? See the graph below.

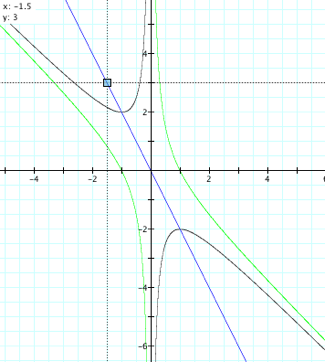
According to this graph:

· For the equation x² + bx +1 = 0 we have two solutions: (-1,2) and (1,-2)

· For the equation 2x + b = 0, if b=3 the line intersects the straight line parallel to the x axis at (-1.5, 3)

Return to my EMAT6680 Class Page

Return to EMAT 6680 Page