By Victor L. Brunaud-Vega
|
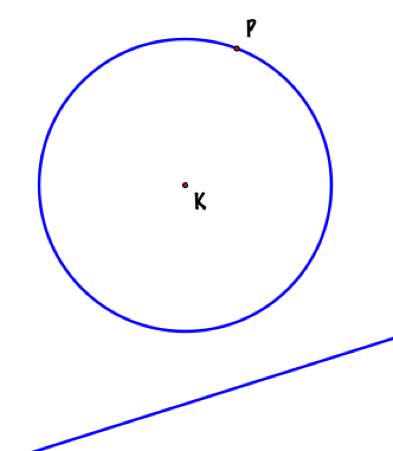
Given
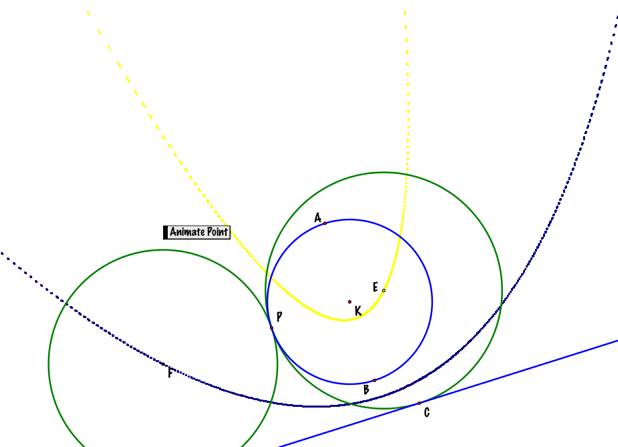
a line and a circle with center K. Take an arbitrary point P on the circle.
Construct two circles tangent to the given circle at P and tangent to the
line. What
do we know about the problem?
One thing that probably is important is that the centers of the two
circles will be part of lines perpendicular to the given line. So, it is reasonable to think that
there is a relationship between P, K, and the given line, through a perpendicular
line. |
|
|
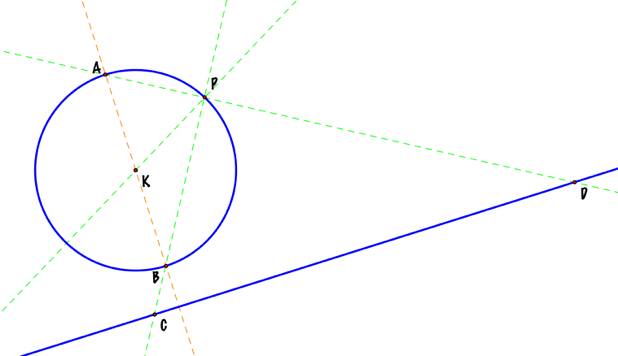
Drawing
a line through K, perpendicular to the given line, we determine the
intersections between this perpendicular line and the given circle: points A
and B. If
I draw lines through points A and P, and points B and P, I will define the
intersections of these lines with the given line at points C and D. |
|
|
|
|
|
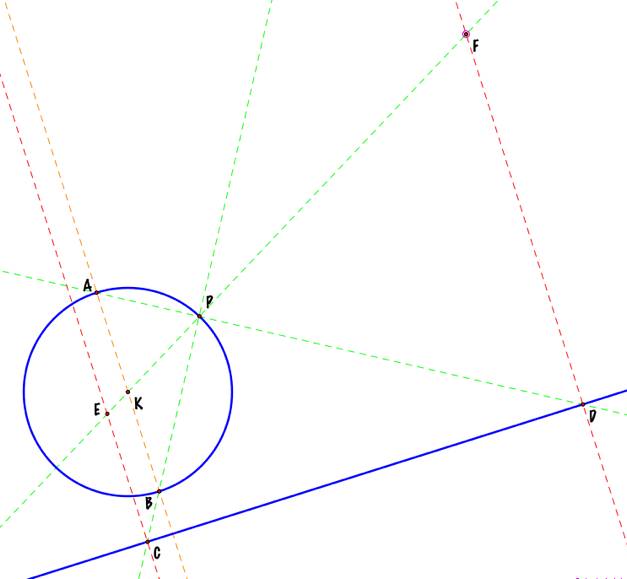
Now,
drawing a line through C, perpendicular to the given line, it will intersect
the line AP at the point E. This
will be the center of one of the circles we are looking for. If I draw a line at point D,
perpendicular to the given line, it will intersect the line BP at point F,
and this will be the center of the other circle we are looking for. |
|
|
|
|
|
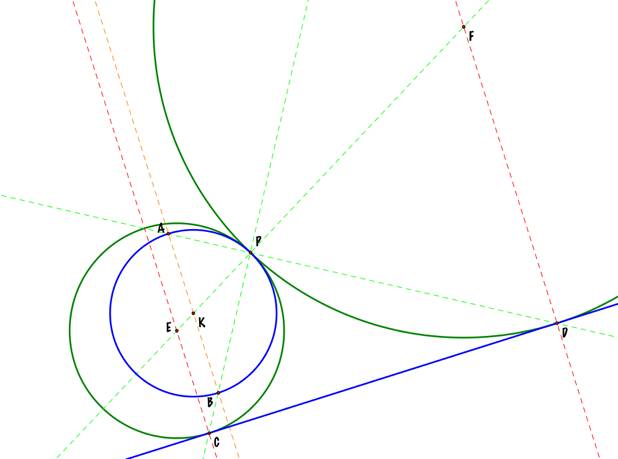
So,
let us construct the circles, centered at points E and F, and with radius EP and
EF, correspondingly. Here
is an animation to see the results and some variations. |
|
|
|
|
|
What
happened with the loci of the centers of the new circles? I made this
animation to find out that the loci of points E and F has a hyperbolic
trajectory. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|