
What actually happens when
we decide to look at the xb-plane instead of the xy-plane?
In the xy-plane our quadratic
equation
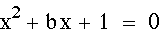 gives us two vertical lines
that represent the roots at those points. When we change our y-axis
to a b-axis, these roots take on the form of a hyperbola. The
xb-plane represents values (x,b) for which this equation hold
true. For each value of b, there are different x values that satisfy
the given equation. With these specific values of a=1 and c=1,
the be values that actually satisfy the equation contain all real
numbers except (-2,2). This means that from -2 to 2, there are
no roots to the given quadratic equation. Therefore, the art of
changing our axis allowed us to make a graphical representation
of the roots of our quadratic equation.
gives us two vertical lines
that represent the roots at those points. When we change our y-axis
to a b-axis, these roots take on the form of a hyperbola. The
xb-plane represents values (x,b) for which this equation hold
true. For each value of b, there are different x values that satisfy
the given equation. With these specific values of a=1 and c=1,
the be values that actually satisfy the equation contain all real
numbers except (-2,2). This means that from -2 to 2, there are
no roots to the given quadratic equation. Therefore, the art of
changing our axis allowed us to make a graphical representation
of the roots of our quadratic equation.
Return

