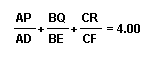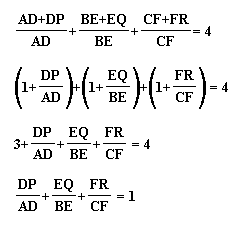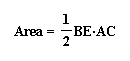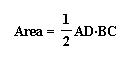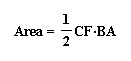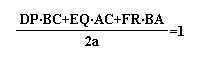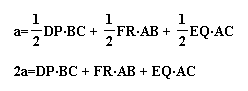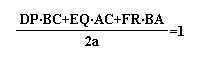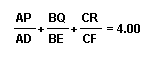Altitudes and the Circumcircle: A Proof
by Kristy Hawkins
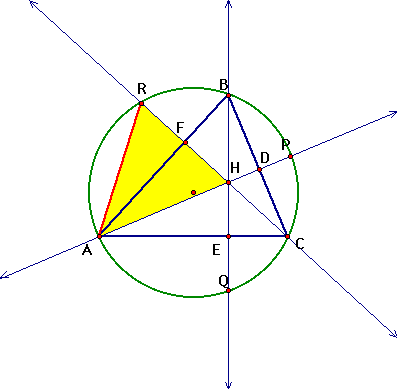
Before we can prove anything, we must know what it
is that we are proving. Begin by constructing any acute triangle
ABC and its circumcircle. Then construct the three altitudes AD,
BE, and CF. Extend each altitude to its intersection with the
circumcircle at corresponding points P, Q, and R.
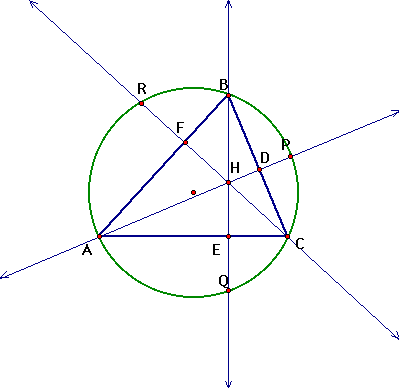 When measuring the lengths of certian segments in GSP,
we can find,
When measuring the lengths of certian segments in GSP,
we can find,
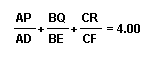 Why did this happen? Let's try to prove that this is
true for all acute triangles!
To begin with, we can simplify the equation by breaking
up AP, BQ, and CR. We can see that AP=AD+DP, BQ=BE+EQ, and CR=CF+FR.
Therefore,
Why did this happen? Let's try to prove that this is
true for all acute triangles!
To begin with, we can simplify the equation by breaking
up AP, BQ, and CR. We can see that AP=AD+DP, BQ=BE+EQ, and CR=CF+FR.
Therefore,
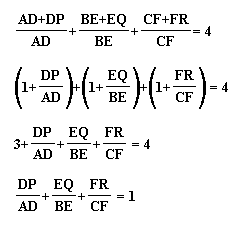 This make our proof more simple! Now this last statement
is all that we have to prove. To continue the proof, let's look
at the area of triangle ABC. This can be expressed in 3 different
ways since we have 3 different altitudes.
This make our proof more simple! Now this last statement
is all that we have to prove. To continue the proof, let's look
at the area of triangle ABC. This can be expressed in 3 different
ways since we have 3 different altitudes.
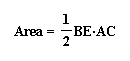
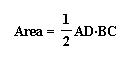
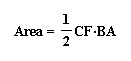 If we substitute these equations into ours we will
simplify it to
If we substitute these equations into ours we will
simplify it to
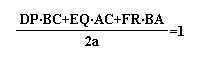 Now if we can show that the numerator of this fraction
is equal to 2a, then we have proven our original claim.
To do this, we will look to congruent triangles. If
we can prove that triangle AHF is congruent to triangle ARF, then
we will be in good shape. We see that both triangles share segment
AF. Also angle AFH is congruent to angle AFR since they are both
right angles by construction. If we show that angle FAH is congruent
to angle FAR, then we have shown that our two triangle are congruent.
Now if we can show that the numerator of this fraction
is equal to 2a, then we have proven our original claim.
To do this, we will look to congruent triangles. If
we can prove that triangle AHF is congruent to triangle ARF, then
we will be in good shape. We see that both triangles share segment
AF. Also angle AFH is congruent to angle AFR since they are both
right angles by construction. If we show that angle FAH is congruent
to angle FAR, then we have shown that our two triangle are congruent.
 Angle FHA is congruent to angle DHC since they are
vertical angles. This means that angle BAP must be congruent to
angle BCR because of the right triangle congruence theorem. We
see that angle RCB corresponds to chord RB. Then we have a picture
like this.
Angle FHA is congruent to angle DHC since they are
vertical angles. This means that angle BAP must be congruent to
angle BCR because of the right triangle congruence theorem. We
see that angle RCB corresponds to chord RB. Then we have a picture
like this.
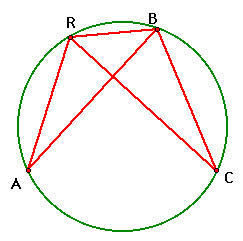 Any two angles corresponding to the same chord on a
circle are congruent, therefore angle RAB is congruent to angle
RCB. This proves that triangles AFR and AFH are congruent by the
ASA congruence theorem.
Since we have shown these two triangles congruent,
we know that in the same way triangle BHD is congruent to triangle
BPD and triangle CHE is congruents to triangle CQE. We can now
express the area of triangle ABC in terms of triangles AHB, AHC,
and BHC.
Any two angles corresponding to the same chord on a
circle are congruent, therefore angle RAB is congruent to angle
RCB. This proves that triangles AFR and AFH are congruent by the
ASA congruence theorem.
Since we have shown these two triangles congruent,
we know that in the same way triangle BHD is congruent to triangle
BPD and triangle CHE is congruents to triangle CQE. We can now
express the area of triangle ABC in terms of triangles AHB, AHC,
and BHC.
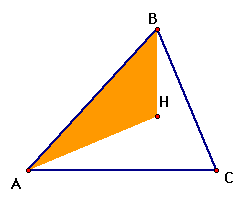
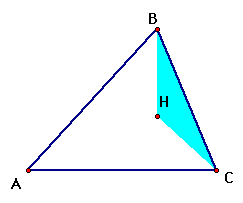
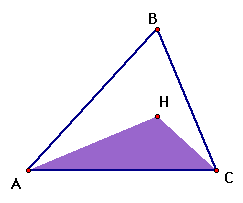
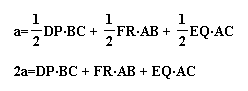 Therefore we have shown that
Therefore we have shown that
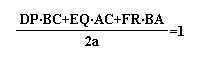 and hence
and hence
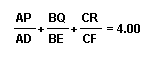
Return