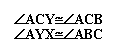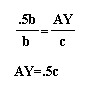Bouncing Barney
by Kristy Hawkins
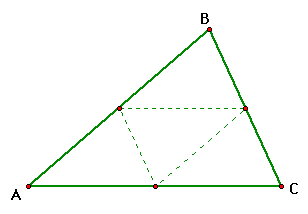
Barney lives in this triangular room ABC.
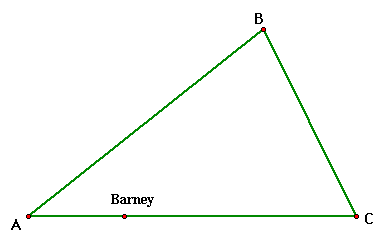He walks from a point on AC parallel to BC. When he
reaches AB, he turns and walks parallel to AC. When he reaches
BC, he turns and walks parallel to AB back to AC. He continues
this process until he reaches his starting point again. How many
times will Barney reach a wall before this happens?
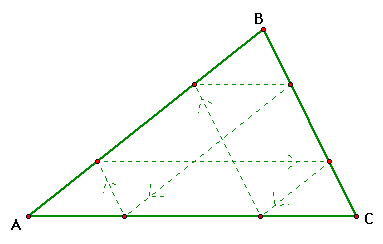Well, when we construct this situation in GSP, it looks
like Barney will return to his starting position after reaching
the sixth wall. Move Barney around in this GSP sketch to see if
you can find any other cases. These two look interesting to me.
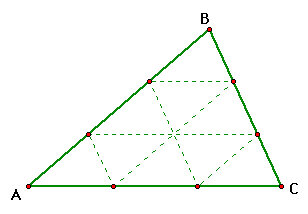What do you think? These might be cases when Barney
is starting at the midpoint of AC or at a point that trisects
AC. I think their might be congruent triangle as well! Let's see
what we can prove!
Let's begin with the most simple case i.e. Barney begins
at the midpoint of AC. Denote AC=b, AB=c, and BC=a.
Prove that Barney returns to his starting point after
two bounces.
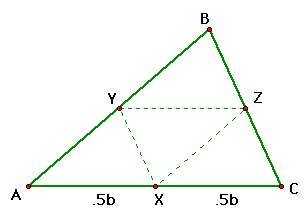First let's prove that triangle AXY is similar to triangle
ACB. This is pretty simple to do because we know that YX is parllel
to BC from the problem. Since this is true,
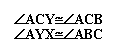by two parallel lines cut by a transversal.
Also, both of these triangles contain angle BAC, and
therefore they are similar.
Since they are similar,
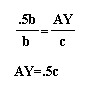In the same way, we can show that BZ=.5a. Since this
is true, when Barney travels from Z parallel to AB, he must land
at X. Therefore he lands at the same place where he began after
two bounces.
This conjecture is also pretty easy to prove wherever
Barney begins on AC by similar triangles and parallel lines.
As I was investigating this situation, I thought about
what would happen if Barney was traveling on lines outside of
triangle ABC. What would that look like? Do you think Barney would
still eventually end up at the same place?
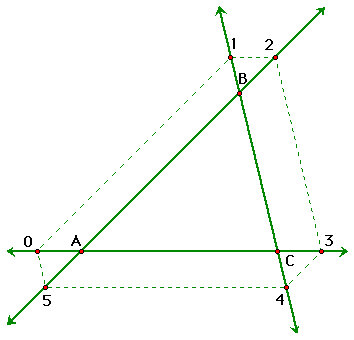He still ends up at the same point after only five
bounces! Can you prove this?
Now let's look at the distance that Barney travels
before he returns to his beginning point.
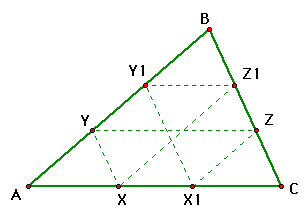At first glance, it looks like the distance that Barney
travels might be equal to the perimeter of the triangle. Would
you agree with this? Let's measure the distances in GSP and see
what we find.
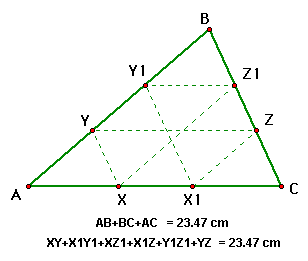It looks like this is true for all triangles. Pretty
cool!
Click here to try other
triangles in GSP.
Return