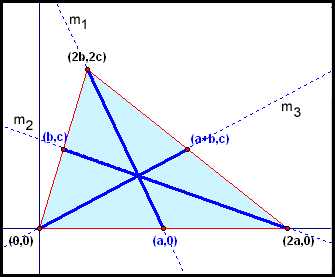
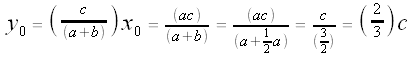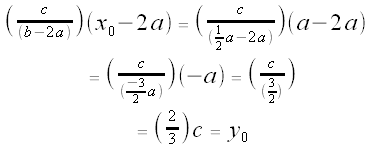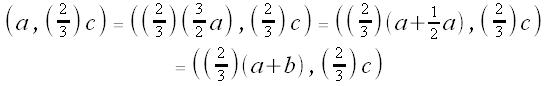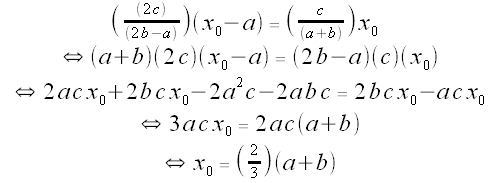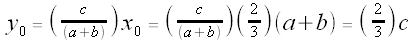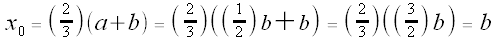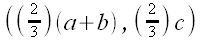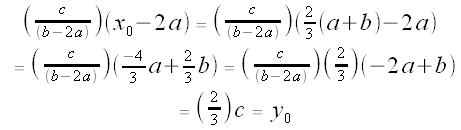The centroid is defined as the point at which the three medians of a triangle meet. Let's prove that the three medians of any triangle really do meet in a single point.
First, let's find equations for the medians of a triangle.
Using the labeling system we have already described, and the midpoint formula, we can find the medians of a triangle:
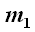 is the line through the points
is the line through the points 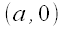 and
and 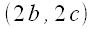 .
.
If 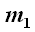 is vertical (i.e., if a = 2b), then
is vertical (i.e., if a = 2b), then
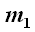 is the line x = a.
is the line x = a.
If 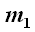 is not vertical (i.e., if a ≠ 2b), then
is not vertical (i.e., if a ≠ 2b), then
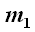 is the line described by:
is the line described by:
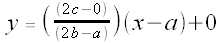
or, more simply,
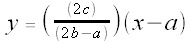
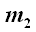 is the line through the points
is the line through the points 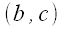 and
and 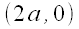 .
.
If 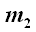 is vertical (i.e., if 2a = b), then
is vertical (i.e., if 2a = b), then
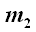 is the line x = 2a.
is the line x = 2a.
If 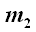 is not vertical (i.e., if 2a ≠ b), then
is not vertical (i.e., if 2a ≠ b), then
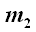 is the line described by:
is the line described by:
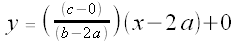
or, more simply,
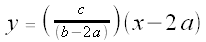
 is the line through the points
is the line through the points 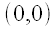 and
and 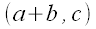 .
.
Note that 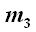 cannot be vertical, since a ≥ 0 and b > 0 (so a + b > 0).
cannot be vertical, since a ≥ 0 and b > 0 (so a + b > 0).
Thus, 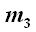 is the line described by:
is the line described by:
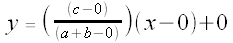
or, more simply,
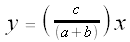
Let's find the point 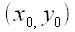 at which
at which 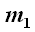 and
and 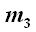 intersect, and then we can determine whether
intersect, and then we can determine whether 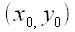 lies on
lies on 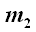 as well. If it does, we will have shown that all three medians intersect in a single point.
as well. If it does, we will have shown that all three medians intersect in a single point.
Case 1: 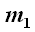 is vertical (i.e., a = 2b)
is vertical (i.e., a = 2b)
Then we must have
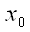 = a
= a
and
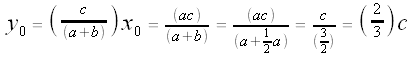
Note that  and
and  can't both be vertical
can't both be vertical
(If they were, then we would have a = 2b and 2a = b,
which implies that a = b = 0,
which contradicts the assumption that a > 0).
So in Case 1, we must have that 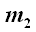 is described by
is described by 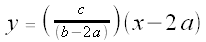
Does our point 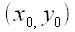 lie on
lie on 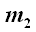 ? Let's find out.
? Let's find out.
The y-coordinate on 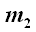 when x =
when x = 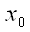 is:
is:
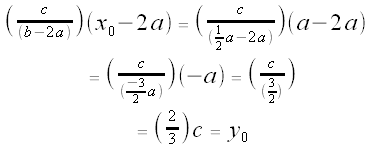
So 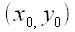 does indeed lie on
does indeed lie on 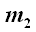 .
.
Thus, in Case 1, the three medians all intersect at a single point.
That point is:
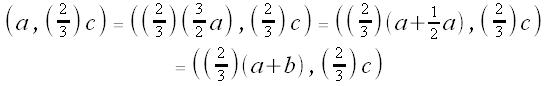
Case 2: 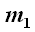 is not vertical (i.e., a ≠ 2b)
is not vertical (i.e., a ≠ 2b)
We need to find a point 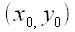 that is on both
that is on both 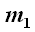 and
and 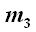
The y-coordinate of both lines must be the same at x = 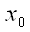 .
.
So we must have:
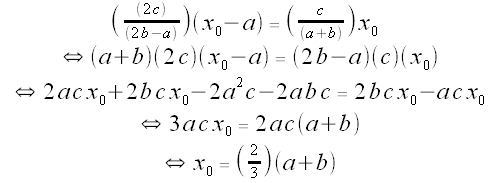
And thus, we must have:
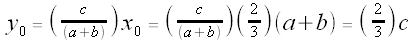
Does our point 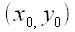 lie on
lie on 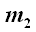 ? Let's find out.
? Let's find out.
Case 2a: 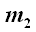 is vertical (i.e., 2a = b)
is vertical (i.e., 2a = b)
Then any point on the line 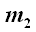 has x-coordinate b.
has x-coordinate b.
Since 2a = b in Case 2a, we have:
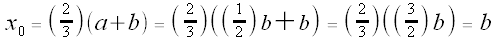
Thus, in Case 2a, the three medians all intersect at a single point.
That point is:
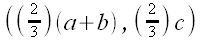
Case 2b: 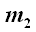 is not vertical (i.e., 2a ≠ b)
is not vertical (i.e., 2a ≠ b)
Then 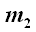 is described by:
is described by:
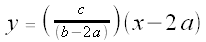
The y-coordinate on 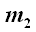 when x =
when x = 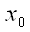 is:
is:
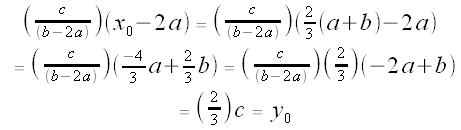
So 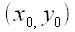 does indeed lie on
does indeed lie on  .
.
Thus, in Case 2b, the three medians all intersect at a single point.
That point is:
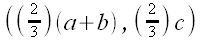
|
So for any triangle, all three medians intersect at a single point, the centroid.
For a triangle whose vertices are (0,0), (2a,0), and (2b,2c)
the coordinates of the centroid are
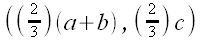
|
Click here to continue.
<< Previous (Introduction) Next (Orthocenter) >>
Return to my page
Return to EMAT 6680 page


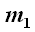 is the line through the points
is the line through the points 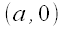 and
and 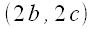 .
.
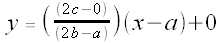
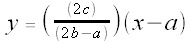
 is the line through the points
is the line through the points 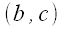 and
and 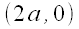 .
.
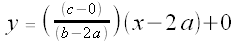
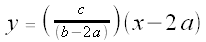
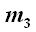 is the line through the points
is the line through the points 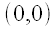 and
and 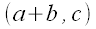 .
.
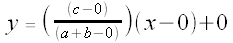
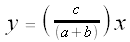
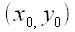 at which
at which 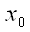 = a
= a