
Tangent Circles
|
|
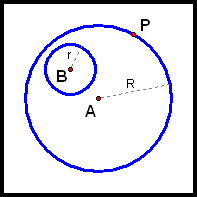
Consider two circles--one with center A and radius R (call it Circle A), and another with center B and radius r (call it Circle B).
Let P be a point on Circle A.
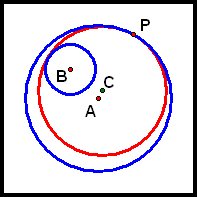
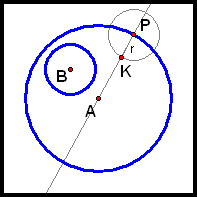
We want to construct a circle, Circle C, that is tangent to Circles A and B such that Circle B lies entirely inside Circle C, like this:
Let C be the center of this tangent circle, and let Q be its point of tangency with Circle B (we will have to determine the locations of Q and C).
Then
Let K be the point on
Then, from (*), we have
CQ = CP
So ΔCBK is isoceles:
Thus, C lies on the perpendicular bisector of
So the tangent circle we want is simply the circle through P,
In this GSP file, you can trace the center C of the tangent circle as P moves around Circle A. What do you see? Move Circles A and B around and adjust their radii. Try as many cases as you can think of, and make some conjectures before clicking here to continue.
|
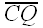 and
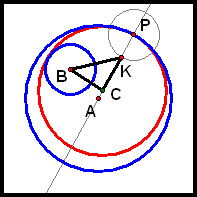
and 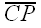 are radii of Circle C, so we must have CQ = CP. (*)
are radii of Circle C, so we must have CQ = CP. (*)
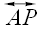 such that AK = R - r and KP = r.
such that AK = R - r and KP = r.
 CB + BQ = CK + KP
CB + BQ = CK + KP
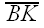 .
.