Tangent Circles
|
|
|
There seem to be four important cases to deal with:
Case 1. R = r
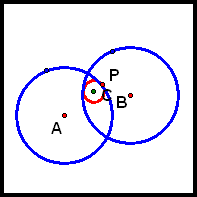
Points K and C are the same point, since K is r units "inside" circle B, whose radius is R = r.
This is true regardless of the location of P, so C always lies on the perpendicular bisector of So the locus of C as P varies is precisely that perpendicular bisector. That is, the locus is a line.
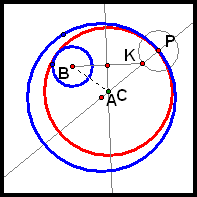
Case 2. R > r Case 2a. Circle A is contained in Circle B.
By construction, we have that BC = CK. So AC + BC = AC + CK = AK = R - r (again, by construction). R and r are both constant, so R - r is constant. So AC + BC is constant. Thus, the locus of C is an ellipse with foci A and B.
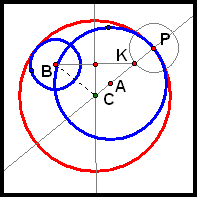
Case 2b. Circle A intersects Circle B in two distinct points.
By construction, we have that BC = CK. So BC - AC = KC - AC = AK = R - r. R and r are both constant, so R - r is constant. So AC - BC is constant. Thus, the locus of C is a hyperbola with foci A and B.
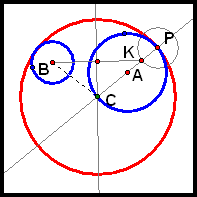
Case 2c. Circles A and B are disjoint.
By construction, we have that BC = CK. So BC - AC = KC - AC = AK = R - r. R and r are both constant, so R - r is constant. So AC - BC is constant. Thus, the locus of C is a hyperbola with foci A and B.
Note that this reasoning was identical to the reasoning we used in Case 2b.
|
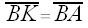 , which is fixed.
, which is fixed.