Investigate each of the following for

Describe each when a=b , a<b ,  a>b.

First, consider the case when a=b=1.

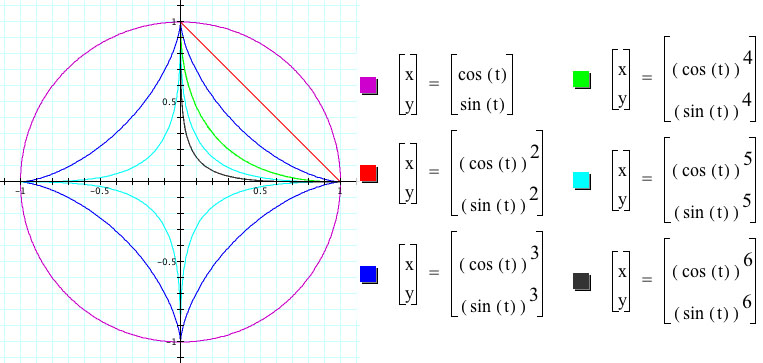I

For  ,

        if n=1, then the graph becomes a circle.

                        Since ,   .

        if n=2, then the graph is a segment in first quadrant.

                        Since ,   .

        if n=3, then because .

                                                            .....

In general, when n is odd, the graph appears in all quadrants, whereas the graph appears in just first quadrant if n is even. Also, the parametric equation satisfies

.

Next, explore when 'a' is changing.

We will observe a graph when n=3. Fix b=1, and change 'a'.

As 'a' is increasing, the graph is stretching horizontally; that is, the width is extending.

Finally, explore the case when 'b' is changing.

Now, observe a graph when n=3. Fix a=1, and change 'b'.

As 'b' is increasing, the graph is stretching verically; that is, the height is extending.

<Appendix>

For  , especially when n=3, that is ,  we call 'astroid'.

If converting this equation into of form f(x, y)=0,

since and  .

Originally, astroid is defined as the trace of a point on a circle of radius r rolling inside a fixed circle of radius 4r or 4/3r.

<Reference>

http://rsp.math.brandeis.edu/3D-XplorMath/Curves/astroid/astroid.pdf

Return to Main Page