-Ceva's Theorem-

Consider any triangle ABC. Select a point P inside the triangle and draw lines AP, BP, and CP extended to their intersections with the opposite sides in points D, E, and F respectively.

　Observe the following file. Drag points A, B, C, and P and explore (AF)(BD)(EC) and (FB)(DC)(EA).

What can you find?

If you want its GSP file, Click HERE!

As you can see, (AF)(BD)(EC) is always the same as (FB)(DC)(EA); that is,

.

Now, I will prove this. However, we should prove the following theorem before our conjecture, which is called the 'Menelaus Theorem.'

<Theorem>

For any triangle ABC, three points P, Q, and R on extended lines BC, CA, AB respectively lie on the same line if and only if

.

<proof>

( =>)              

Like above figure, suppose P, Q, and R lie on the same line and let p, q, and r is the lengths of perpendicular line from each vertex A, B, and C, respectively. Then, by the feature of similar triangles,

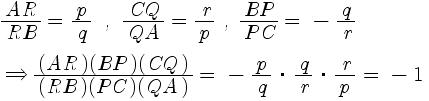
( <= ) Suppose holds.

If the line passing through points P and Q meet BC at the point P', since R, Q, and P' lie on the same line,

.

Divide this equation by . Then,

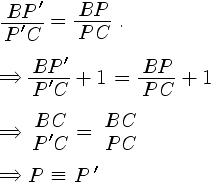
Therefore, points R, Q, and P lie on the same line.        

Now, prove Ceva's theorem.

For any triangle ABC, lines AD, BE, and CF connecting each point A, B, and C and D, E, and F on each side BC, CA, and AB, respectively meet at a point P if and only if the following equation holds;

.

<Proof>

( => ) Suppose that three lines AD, BE, and CF meet at a point P. Then, by previous theorem,

.

Multiply two equations, then

( <= ) Suppose and a line BE meets a line AD at a point P and a line segment CP meets side AB at a point F '. Then, three line segments AD, BE, and CF meet at a point P, so

 .

Divide this equation by . Then,

.

Therefore, F = F ' .

Generally, Ceva's Theorem is true when a point P is outside triangle ABC.

Explore below file. Drag the points A, B, C, and P.

If you want GSP file, Click HERE!

Return to Main Page