Department of Mathematics and Science Eduacation
Allyson Hallman
A little bit of work with circumcenters and altitudes. Need a review? check out library.
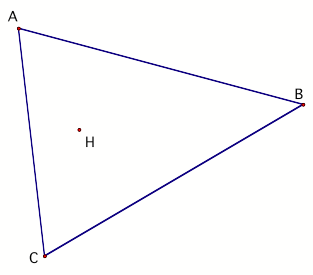
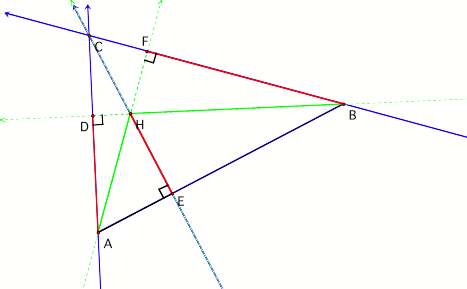
Consider any triangle and its orthocenter, H.
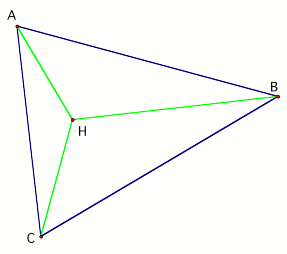
We can form the secondary triangles, AHB, AHC, and BHC. It turns out that the orthocenter of each of our secondary triangles lies of on one of the vertices of the original triangle. Check it out using orthocenter tool in GSP.
But why is this so?
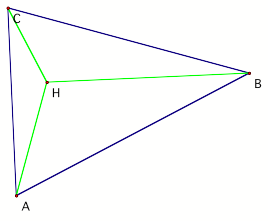
Consider the orthocenter of triangle HAB. The green segments are the contained in the altitudes (perpendicular lines from a vertex to the opposite side) of the original triangle. Let’s extend them.
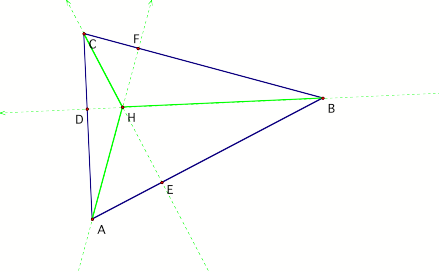
Altitude 1: We know that CH is perpendicular to AB at E, so the altitude of DAHB dropped from H is HE, which is contained in line CE. Altitude 2: Next, what is the altitude dropped from A? BH is defined as perpendicular to CA at D, so the altitude of DAHB dropped from A is AD, which is contained in line CA. Altitude 3: Next, what is the altitude dropped from B? AH is defined as perpendicular to CB at F, so the altitude of DAHB dropped from B is BF, which is contained in line CB.
Red segments are the three heights of DHAB, as we found above. To find the orthocenter of DHAB we need to consider where the lines contining those segments meet. That is where do CA, CA, and CB meet? As you can see from the blue lines pictured to the right (an frankly, as is obvious from the question) the lines meet at C. And so C is the orthocenter of DHAB. By similar reasoning we can show that B is the orthocenter of DHAC and A is the orthocenter of DCAB.
So that’s pretty neat. What other relationships might exist here? What about the circumcenters of our three secondary triangles?
Looks like a good time already.
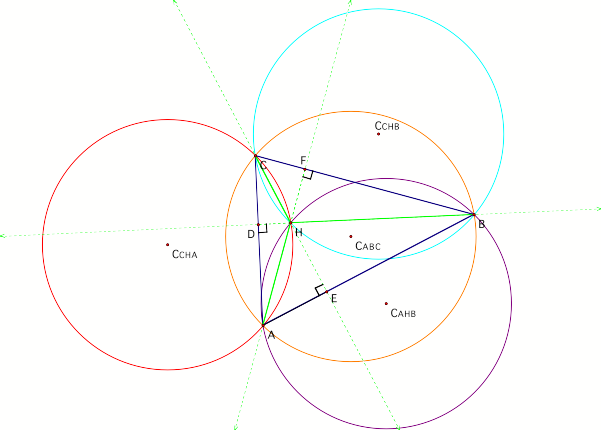
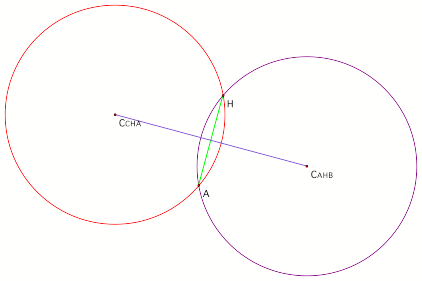
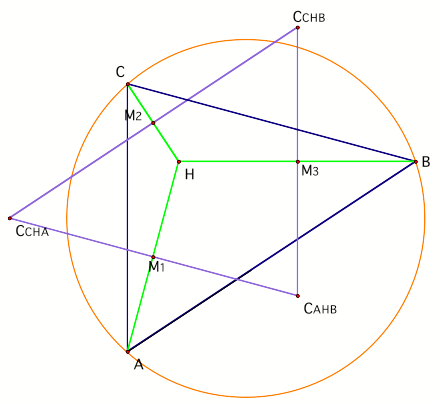
Construct segment CCHACAHB . I know it looks crazy. Let me “zoom-in for you I hope you are able to recognize the construction of a perpendicular bisector. HA is bisecting CCHACAHB at a right angle. Seems trivial but oh my goodness its not (It’s the key, the one I was searching for all day and most of last week!!!!)
We will name the midpoint of CCHACAHB M1. Likewise we show that we have midpoints M2 of CCHACCHB , and M3 of CBHACCHB. Ok, now yes, the diagram is kind of wacky, so let’s eliminate a few things for the picture. Now, we want to show that the circumcenters of our secondary triangles are equidistant from the orthocenter of our original triangle.
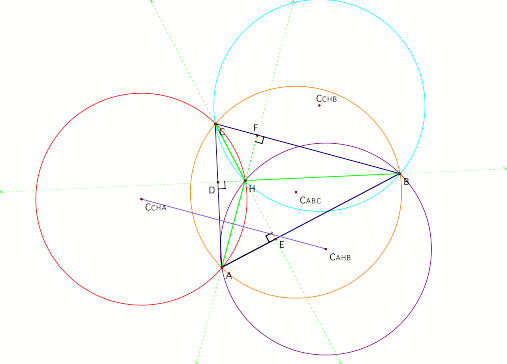
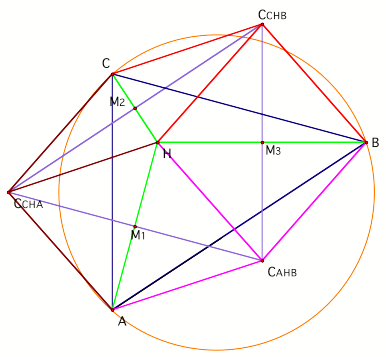
Now we have constructed the segments connecting each of the three circumcenters to vertices of its triangle. CAHB connected with pink segments to A, H, and B. CCHA connected with brown segments to C, H, and A. CCHB connected with red segments to C, H, and B. We know that HA is the perpendicular bisector of CCHA CAHB. Since the base of triangle CCHA CAHB A was bisected at a 900 angle we know that triangle CCHA CAHB A is isosceles. Thus ACCHA is congruent to ACAHB. We can then conclude that the brown segments and pink segments are congruent. By similar logic and the transitive property of congruence, we are able to show that the brown, pink, and red segments are congruent. Thus our circumcenters of the secondary triangles are equidistant from the orthocenter of the original triangle.
What does that mean? The orthocenter of the original triangle is the circumcenter of the of the triangle whose vertices are circumcenters of the secondary triangles. That’s a mouthful.
A problem for your own fun and amusement: Is the converse true? The circumenter of the original triangle is the orthocenter of the of the triangle whose vertices are circumcenters of the secondary triangles.
Return home.