|
A brief libraray of
some useful definitions, diagrams, and constructions Allyson
Hallman Click
here for to access all tools in Geometer's Sketchpad |
||
|
Return to: Explorations
with Sine and Cosine Varying
Coefficients of Quadratic Equations Locus
of Vertices of Parabolas Explorations
of Triangle Circumcenters Orthocenters
and Circumcenters, oh my! Similiarity
of Pedal Traingles |
Concurrent Lines & Point of
Concurrency
Concurrent lines
intersect in a single point and that point of intersection is the point of
concurrency |
|
|
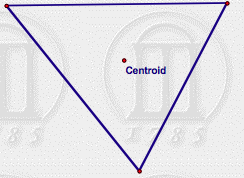
Centroid
Point of
concurrency of medians of a triangle |
|
|
|
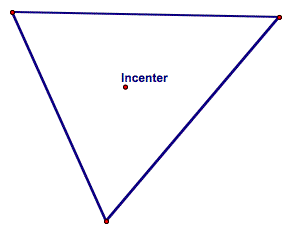
Incenter Point of concurrency
of angle bisectors of a triangle |
|
|
|
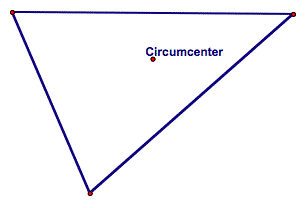
Circumcenter Point of concurrency
of perpendicular bisectors of sides of a triangle |
|
|
|
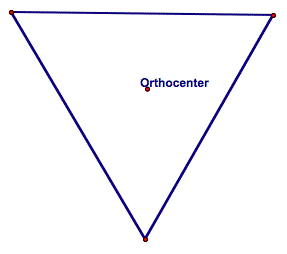
Orthocenter Point of
concurrency of the altitudes of a triangle |
|
|
|
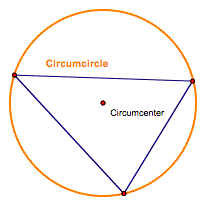
Circumcircle Circle whose center
is the point of concurrency of the perpendicular bisectors of the sides or a
triangle and whose radius is the distance from that point to any vertex of
the triangle |
|
|
|
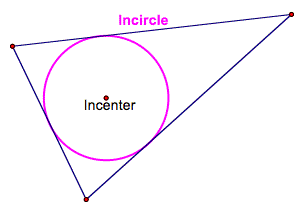
Incircle Circle whose
center is the point of concurrency of angle bisectors of a triangle and whose
radius is the distance from that point to any side of the triangle. |
|
|
|
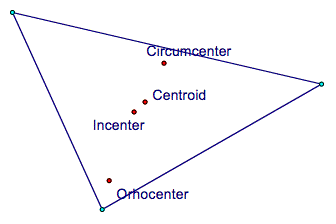
Triangle Centers C = Circumcenter I = Incenter H = Orthocenter G = Centroid |
|
|
|
Triangle Centers with Euler Line Line containing
circumcenter, orthocenter, and centroid |
|
|
|
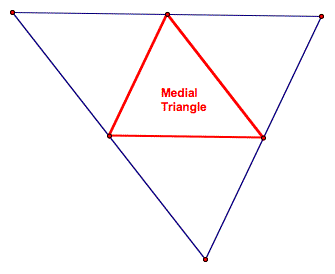
Medial Triangle Triangle whose
vertices are the midpoints of the sides of another triangle |
|
|
|
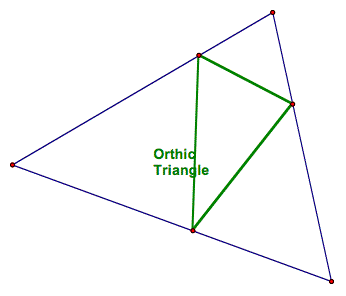
Orthic Triangle Triangle whose
vertices are the feet of the altitudes of another triangle *feet?? Click here. |
|
|
|
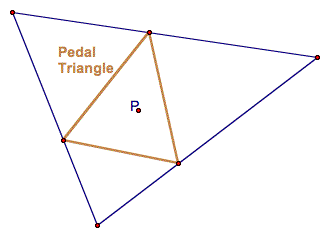
Pedal Triangle Triangle whose vertices are the feet of
the perpendiculars from any point P to each side of the triangle |
|
|
|
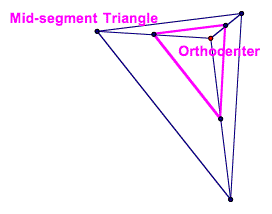
Orthocenter, Midsegment Triangle Triangle whose vertices are the midpoints
of the segments connecting the orthocenter to each vertex |
|
|
|
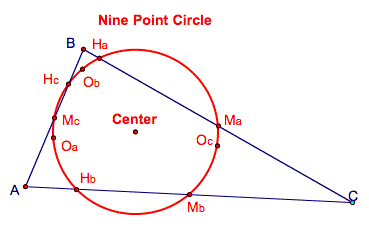
Circle that
passes through the midpoints of each side of a triangle (Ma, Mb,
Mc), feet of the altitudes of that triangle (Ha, Hb,
Hc), and the midpoints of the segments that connect the vertices
of that triangle to its orthocenter (Oa, |
|
|
|
Equilateral Triangle Triangle with
all three sides congruent |
|
|
|
Isosceles Triangle Triangle with at
least two sides congruent |
|
|
|
Square Quadrilateral
with four congruent sides and 4 congruent angles |
|
|
|
Regular Pentagon (given radius or side) Polygon with
five congruent sides |
|
|
|
Regular Hexagon (given side) Polygon with six
congruent sides |
|
|
|
Regular Octagon (given side) Polygon with eight congruent sides |
|
|
|
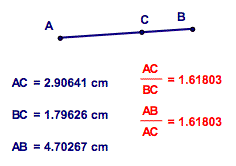
Golden Ratio |
|
|
|
Locus of a vertex of a fixed angle that
subtends a fixed segment |
|
|
|
Trisect a segment Divide a segment into three congruent
parts |
|
|