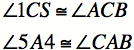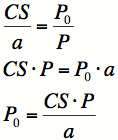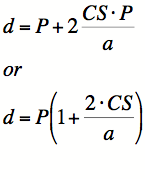Department of Mathematics and Science Education
	Allyson Hallman
Bouncing Barney
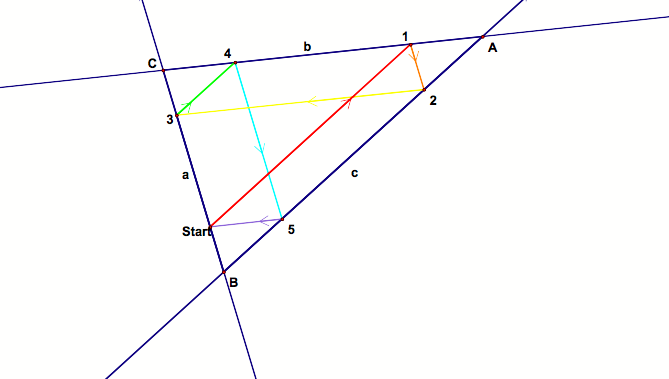
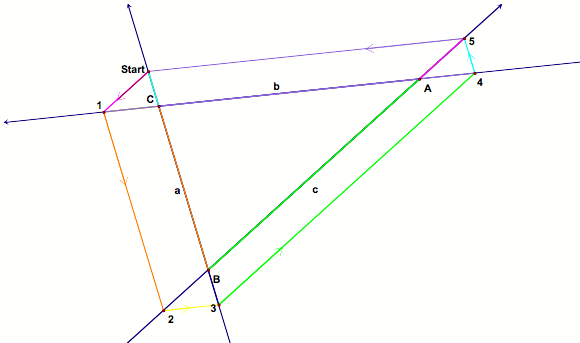
Barney is in the triangular room shown here. He walks from a point on BC parallel to AC. When he reaches AB, he turns and walks parallel to BC. When he reaches AC, he turns and walks parallel to AB. Prove that Barney will eventually return to his starting point. How many times will Barney reach a wall before returning to his starting point?
				Explore in GSP.
Path above is “Start-red-1-orange-2-yellow-3-green-4-blue-5-purple-Start.”
Ok, This looks yucko. Let’s find something easy.
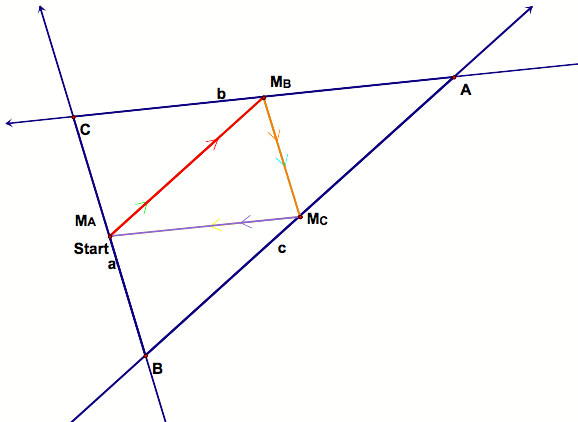
Case #1: Suppose Barney Starts at a midpoint. Check it out.
Starting at midpoint of side a, called MA and constructing a parallel line to side c we will in fact intersect side b at its midpoint MB. We know that a line that intersects two sides of a triangle and that is parallel to the third divides those two sides proportionally. Thus, if side a is intersected at its midpoint, then side b will also be intersected by the parallel line at its midpoint. By the same logic, our next two parallel lines will hit the midpoint of side c, MC, and the midpoint of side b, MB, respectively. Thus good ole Barney has returned exactly to where he started and the path he has traveled forms the medial triangle.
Yes, but how far did he go? Well this is really quite simple. (thankfully, since it will be the last simple thing we do today.)
If the segment connects the midpoints of two sides of a triangle (by the way called a mid-segment), then that segment is (parallel which we already knew) and half the length of the third side.
So Barney’s distance is
, which is half the distance of the perimeter of the triangle.
Is this always the case? Why no, of course not. (that would be too easy)
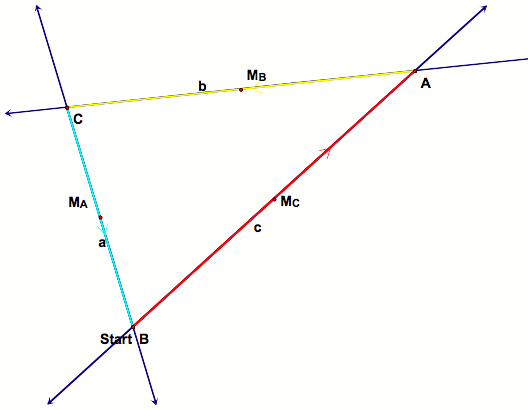
Case #2: Suppose Barney starts at a vertex of the triangle.
This is really quite boring. Obviously Barney’s path becomes the original triangle itself. And so the distance he travels is simply equal to the perimeter of the triangle.
So when does it get interesting?
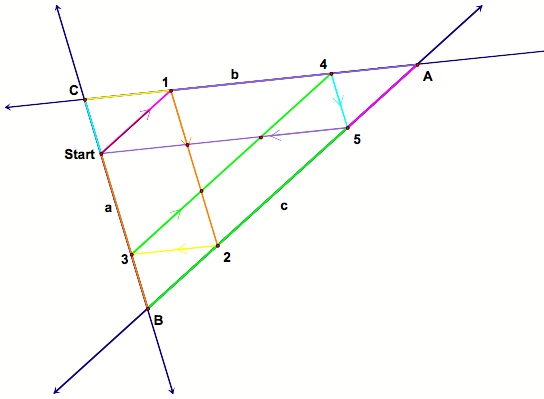
Case #3: Suppose Barney starts at a point on the side of the triangle that is neither a vertex nor a midpoint of a side. (Finally something fun.)
The nice thing is that we have a zillion (yes, and I counted them) pairs of parallel lines, which gives us a bunch of parallelograms. And if we have parallelograms, then we know that the opposite sides are congruent.
The segments with the matching colors are congruent!! (What you don’t believe me? There’s a proof below, but trust me, you’ll wish you’d just believed me)
Let d = distance Barney travels.
				Just adding his path.
				Substitution using the pretty colored statements above.
				Fun with the associative property of addition.
				Substitution with segment addition.
				Renaming sides of our original triangle.
Thus the distance Barney travels is equal to the perimeter of the triangle.
So, you think we’re done? You’re wrong; there’s more.
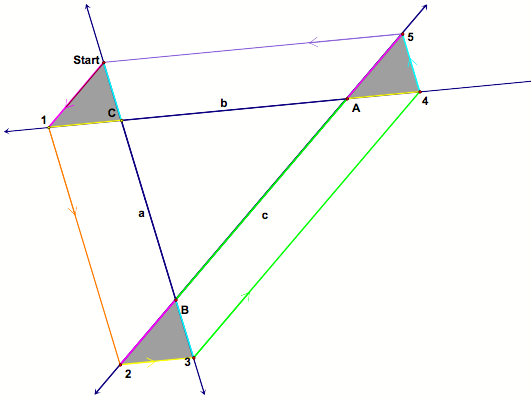
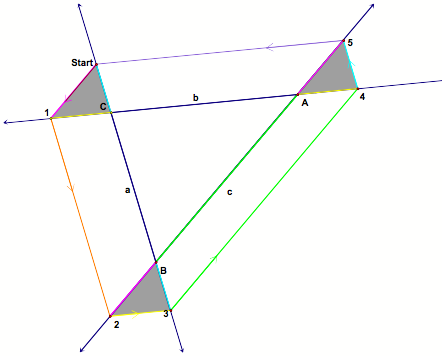
Case #4: Suppose Barney starts at a point on the exterior of the triangle.
See the little triangles? We need to show they are congruent. Want to see GSP?
Again, let d = distance Barney travels.
Can substitute something here? Gosh I hope so.
				Adding segments of Barney’s Path.
				Substituting from the steps above.
				A little color coding to help us see what’s going on here.
We know a + b + c = perimeter of original triangle. Call this P.
We know that pink + blue + yellow = perimeter of one of our gray triangles. Call this P0. And we have 2 of these, so 2P0. A little substitution gives us:
d = P + 2P0
Can we find an expression for P0 in terms of P? (Probably.)
We know that our original triangle is similar to our gray triangles.
			Because vertical angles are congruent Because corresponding parts of congruent triangles are congruent. By AA Triangle Similarity Postulate. Since the gray triangles are congruent, each is similar to the original triangle.
Since the gray triangle is similar to the original triangle, the ratio of their perimeters is equal to the ratio of their sides.
Ratio of sides is CS : a. Setting up a proportion with their perimeters gives:
		And so finally we have the distance Barney Travels when he starts on the exterior of the triangle is d = P + 2P0 And all in terms of P this equals:
Go home or continue to second part of final.