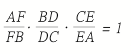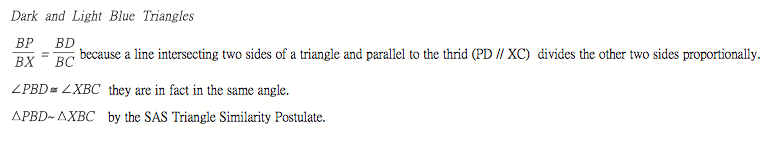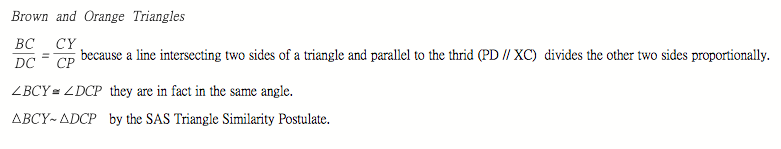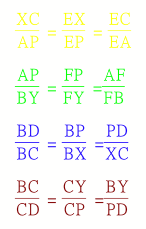Department of Mathematics and Science Education
	Allyson Hallman
Ceva’s Theorem: What’s the point?
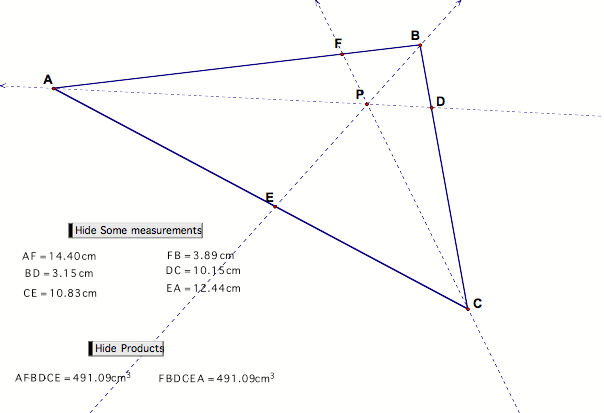
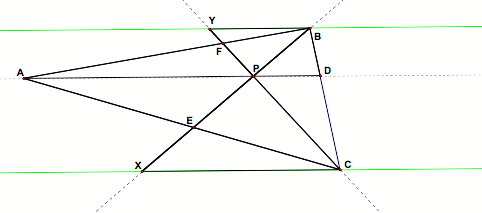
Consider any triangle ABC. Select a point P inside the triangle and draw lines AP, BP, and CP extended to their intersections with the opposite sides in points D, E, and F respectively.
Need a picture? I thought you might.
			Explore in GSP.
Given that the two products are always the same, we can conclude that the ratio of those products equals 1. Can we prove it? Why sure!! (mind you, 4 hours ago, I would have said no.)
Ceva’s Theorem: If the three line segments joining the each vertex of a triangle to any
point on the opposite sides are current, then
We can see that we have proportions going on, so that should be a clue that we are look for similar triangles. How might we find some? Why by constructing parallel lines of course.
Construct two lines parallel to AD, one of which passes through point B and one of which passes through point C.
You might be wondering, “How did we know to construct these specific parallels?” Well, after hours of constructing many and realizing that most are useless you are left with these two parallels.
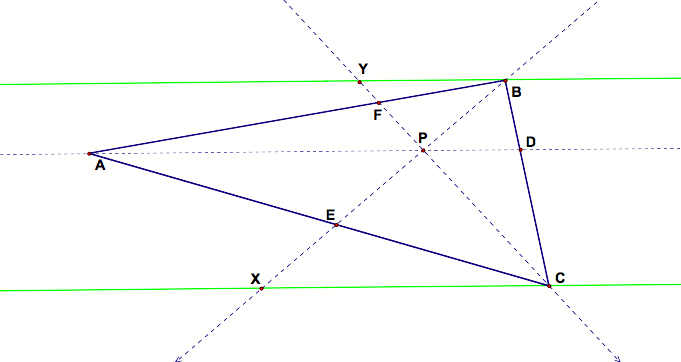
Now we need to look for some similar triangles.
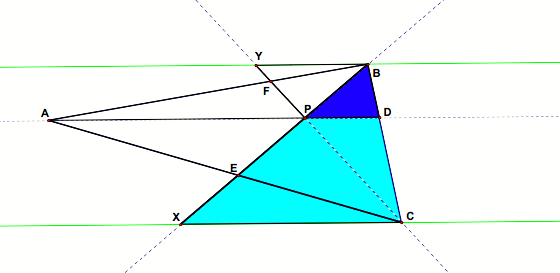
The yellow triangles are similar and the green triangles are similar. Why? I am so glad you asked:
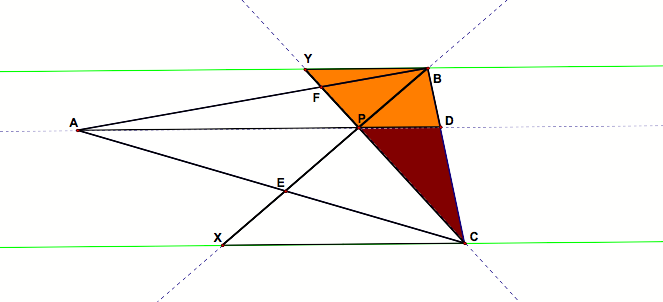
But wait, there are more similar triangles:
Yes, there’s one more.
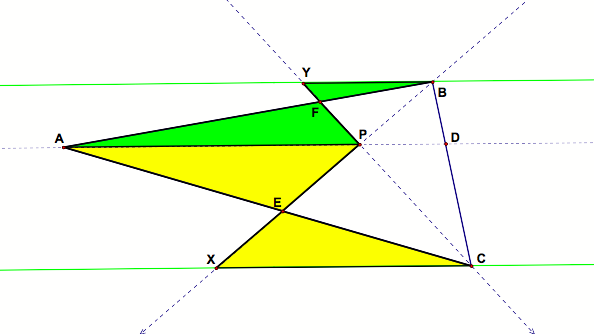
From these four pairs of similar triangles we have the following proportions:
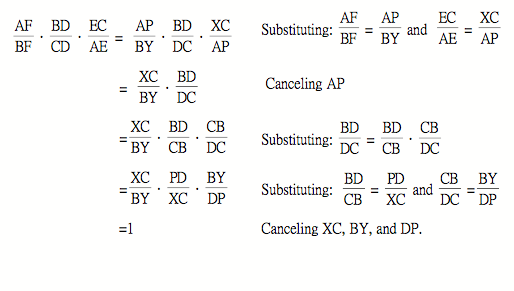
And finally using all those similar triangles we can prove our theorem:
		Want to see all of that in one pretty GSP?
What happens if our point P moves outside of the triangle? Will our theorem hold? Check it out here in GSP.
Go home or to the first part of the final.