Allyson Hallman
Exploration of Pedal Triangles
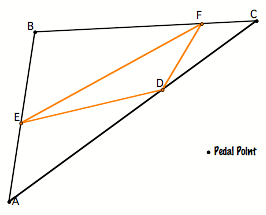
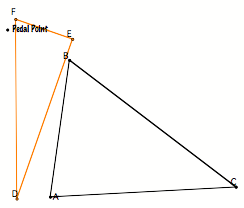
First let us consider the pedal triangle of any triangle (what’s this?): Note that both the pedal point and the pedal triangle can be in the interior or exterior of the triangle. (Pedal triangles are pictured in orange.)
Let us first examine the relationship between the pedal point and the centers of a triangle.
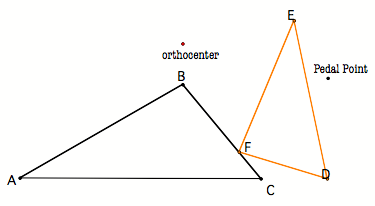
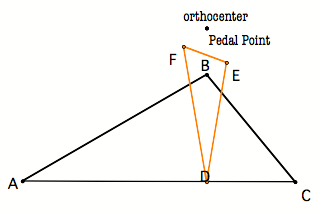
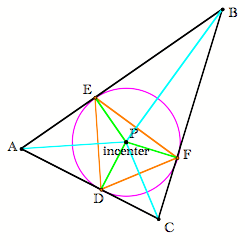
Suppose the pedal point is the orthocenter of the triangle.
Click to explore the “motion” in GSP.
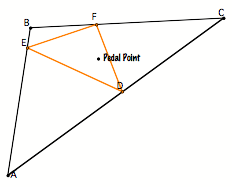
What do we know about the pedal triangle (orange) pictured on the right?
The pedal triangle is the triangle whose vertices are the feet of the perpendiculars from any point P to each side of the triangle or more simply we can say it’s the triangle whose vertices are the intersections of the perpendicular lines drawn from any point P with the side of the triangle to which they are perpendicular. The orthocenter is the point where the altitudes of triangle meet. That is, it’s the point where the lines containing the perpendiculars drawn from each vertex meet. If that point P becomes the orthocenter, then the perpendiculars drawn from P to the sides of the triangle are in fact contained in the altitudes of the triangle, and the feet of the altitudes then form the intersections of the perpendiculars drawn from P with the sides of the triangle. Finally, we can see that the feet of the altitudes are the vertices of the pedal triangle. But Wait!! The triangle whose vertices are formed by the feet of the perpendiculars of the original triangle is called the Orthic Triangle. Conclusion #1: If the pedal point is the orthocenter, then the pedal triangle is the orthic triangle.
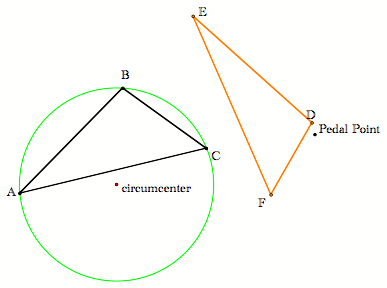
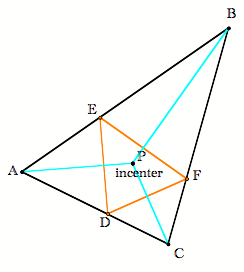
Next, we suppose the pedal point is the circumcenter of the triangle.
Click to explore the “motion in GSP.
What do we know about the pedal triangle (orange) pictured on the right?
Call the pedal point which is also the circumcenter, P.
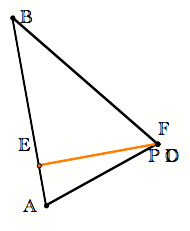
We know that circumcenter is equidistant from the vertices. So We want to examine the perpendicular drawn from P to AC. Consider the triangle
Drop a perpendicular from P, which will intersect the opposite side at point D, as expected. tells us that we have an isosceles triangle. A perpendicular dropped from the vertex angle of an isosceles triangle to the opposite side will be the perpendicular bisector of that side. Thus D is the midpoint of AC. By similar argument, E is the midpoint of AB and F is midpoint of BC. Thus is the medial triangle of triangle .
Conclusion #2: If the pedal point is the circumcenter, then the pedal triangle is the medial triangle.
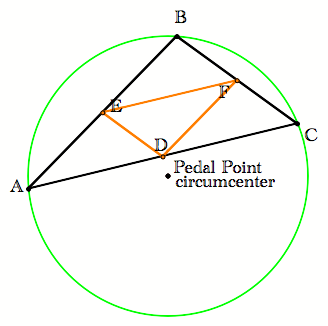
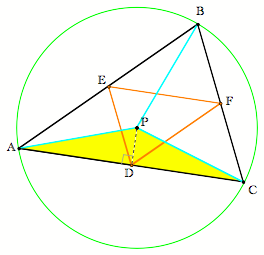
Suppose the pedal point is the incenter of the triangle. Click here to explore this motion in GSP.
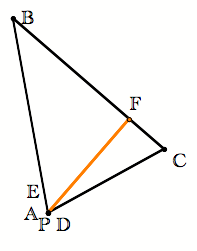
We know that the incenter, in this case P, is equidistant from the sides of the triangle. We measure the distance from a point to a line by dropping the perpendicular from the point to the line. E, D, and F are the intersections of the perpendiculars drawn from P with the three sides of the triangle. So . The distance from P to each vertex of the pedal triangle is the same and so, P is the circumcenter of .
Drop a perpendicular from P, which will intersect the opposite side at point D, as expected. tells us that we have an isosceles triangle. A perpendicular dropped from the vertex angle of an isosceles triangle to the opposite side will be the perpendicular bisector of that side. Thus D is the midpoint of AC. By similar argument, E is the midpoint of AB and F is midpoint of BC. Thus is the medial triangle of triangle .
Conclusion #3: If the pedal point is the incenter of the original triangle, then the pedal point is circumcenter of pedal triangle.
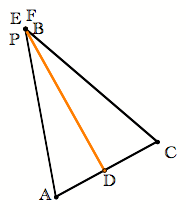
Next, we suppose the pedal point is one of the vertices of the triangle.
Consider the three cases. Want to check it out in GSP?
Pedal point moves to A		Pedal point moves to B			Pedal point moves to C
It should be pretty easy to see that when the pedal point is on a vertex of the triangle that the pedal triangle is degenerate (all its vertices are collinear). Why would this happen? Are there any other conditions under which it would happen?
If the pedal point is on the vertex of the triangle, then the pedal point is in fact on two sides of the triangle. Then construct a perpendicular through P to those two sides, which means that P itself will be the intersections of those perpendiculars and those two sides. Thus two vertices of our pedal triangle are exactly on top of P. It only remains to find the intersection of the perpendicular drawn to the third side of the triangle with that side. Thus when we connect the three vertices of the pedal triangle we are really only connecting P (which is representing two of our vertices of the pedal triangle) to the foot of the perpendicular to the third side (the third vertex of our pedal triangle). And so all we have is a line segment, our degenerate pedal triangle.
Conclusion #4: If the pedal point is on the one of the vertices of original triangle, then the pedal triangle is degenerate.
And those are not the only conditions where the pedal triangle is degenerate. When the pedal point is on the circumcircle of the original triangle we also have degenerate pedal triangle. Check it out.
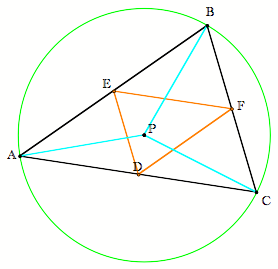
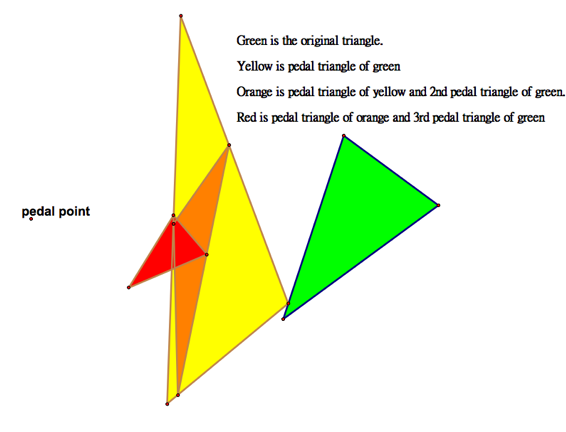
But here is the really interesting cool fun part that I am oh so excited I finally figured out. Look at the pedal triangles below.
Through the sheer wondrous power of observation you may notice that green and red triangles appear to be similar. Let’s check this out with some measurement. Click here to explore tutorial in GSP. So we have the idea that they are similar, how can we prove that they are????
LIKE THIS. A tutorial of the proof with corresponding diagrams has been constructed for you in GSP. Don’t skip this one, just thinking it’s another boring GSP file. This one is awesome and it took me a whole day in the middle of finals week when I should have been studying for abstract. So please please, click the link.
Did you click the link?? Wasn’t it fabulous and well worth the plummeting of my grades in all other courses? Worn out from the intensity? Go home.