Hamilton
HardisonÕs Exploration of
Assignment 3: Locus of Vertices of Parabolas of the Form y = x2 + bx + 1
From
Jim WilsonÕs
Assignment page: Consider the
locus of the vertices of the set of parabolas graphed from 
. Show that the
locus is the parabola 
.
By using a graphing utility, it appears that the vertices of
these parabolas do lie along another parabolic curve.
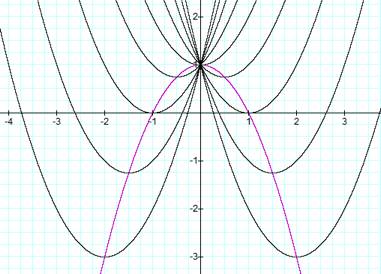
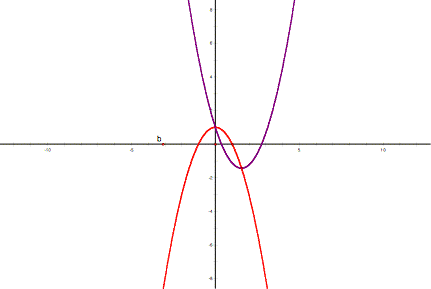
We can support this conjecture by tracing the vertex of the
parabola 
, using geometerÕs
sketchpad. The red parabola in the
image below was created by tracing the vertex and appears to be 
.
We
can now explore the situation algebraically.
The
vertex of any parabola, 
, lies on the parabolaÕs line of symmetry, 
. So each vertex
for a parabola 
has 
as itÕs
abscissa. The ordinate of each
vertex is
.
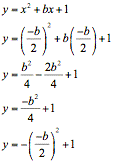So for each value b, we have a
vertex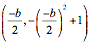 
. Thus, vertices
of the parabolas trace out the curve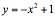 
.
In general, the vertices of 
, have abscissa 
. The ordinate
of a given vertex is
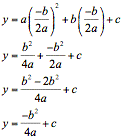
So for any quadratic function
, the locus of the vertex as b varies will be given by 
.
For calculus students: What is the locus of the point on a
parabola 
whose tangent line has slope one? Is there an algebraic generalization? A rough sketch of a solution is here.
Return
to Hamilton Hardison's Page