
HamiltonHardison’s Exploration of
Assignment 7: Tangent Circles and Conics
From
Jim
Wilson’s website:
Assignment
7 begins with a walkthrough of the construction of a circle tangent to two
given circles. Two related constructions
are suggested. See the GSP Sketch here.


The
Purple and Blue figures are the loci of the centers of the red tangent
circles. By combining both constructions
in one GSP sketch, we can explore the different cases for the loci. The construction lines have been hidden and
the tangent circles are dashed in the following images in order to remove
clutter.

In this case both loci appear to be ellipses.
They appear to have the same foci:
the centers of the two given green circles.
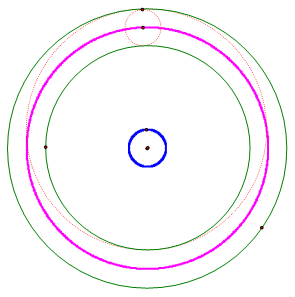
If the two given circles are concentric, it appears that both loci are circles
that share the center of the two original circles. The blue “circle” appears to have a radius
equal to the smaller red tangent circle.
The purple “circle” appears to have a radius equal to the larger red
tangent circle.

As the interior green circle becomes tangent to the larger green circle, the blue
ellipse seems to collapse, while the purple remains an ellipse. At this point of tangency, one of the two red
tangent circles merges with the larger green circle.

The blue locus reappears as a hyperbola, once the circles intersect at two
distinct points. The purple remains an
ellipse.

As the smaller green circle moves further out, the purple ellipse collapses and
the second red tangent circle merges with the larger green circle. The blue locus remains a hyperbola.

Once the green circles have no common point of intersection, the purple locus
emerges as a hyperbola. The blue locus
remains a hyperbola. Both loci seem to
share the same focal points, still the centers of the two green circles.
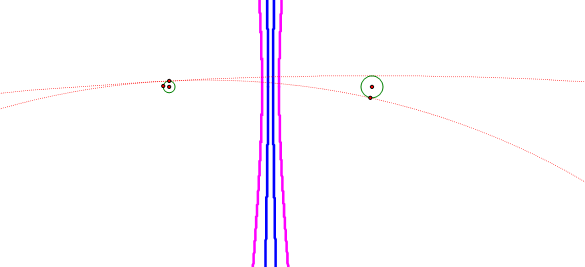
As the circles become further apart, the hyperbolas seem to become more
linear. The red tangent circles grow to
be extremely large. I have not found a
case when the locus appears to be a parabola, which is surprising with so many
conic sections floating around in this sketch.
Returnto Hamilton Hardison's Page