Investigating Polar Equations

By Sharon K. O’Kelley

Part One

Let us begin with an investigation of a basic polar equation….

Below are several graphs of this polar equation when b and k are varied. Let’s see if we can find some patterns.

1. When b = 1 and k =1, the result is a circle.

2. When b = 1 and k =2, the result is a figure with four petals.

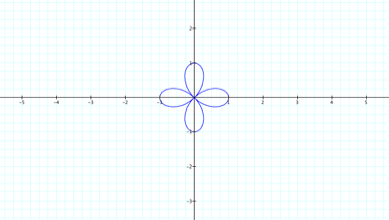
Could it be that when k is even, the number of petals is twice the value of k? If that is the case, then when k=4, the figure will have 8 petals. Let’s check it out….

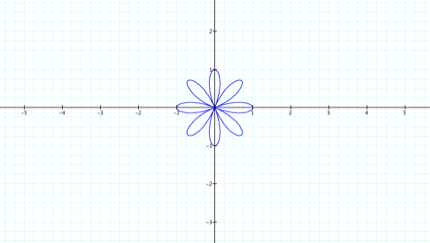
(Notice that the tips of the horizontal and vertical petals are at 1 and -1.)

3. What would happen if we changed b to a value other than 1? Let’s experiment with the last equation and make the value of b equal to 3.

Notice that the horizontal and vertical tips are now at -3 and 3 which means the original figure has been stretched by a factor of 3.

Does this mean that if b is less than 1, it will shrink? Let’s see….

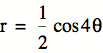
4. What would happen if k were odd? Let’s try one….

In this case, it appears that the number petals corresponds to the value of k so that should mean that if k =7, then the figure should have 7 petals.

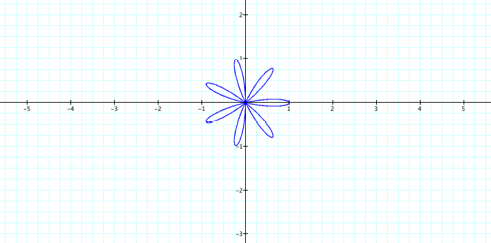
Based on the previous work, we can guess that if b is equal to any number other than 1 the figure will stretch or shrink. A case in point….

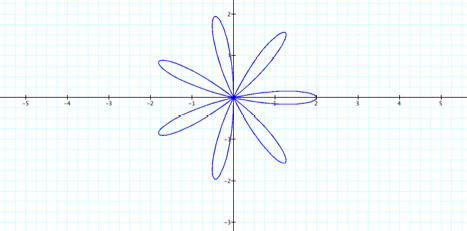
Part Two

Let’s make it interesting and investigate the polar equation...

1. Let’s make a = 1, b = 1, and k = 1.

2. Now, let’s make a = 1, b = 1, and k = 4.

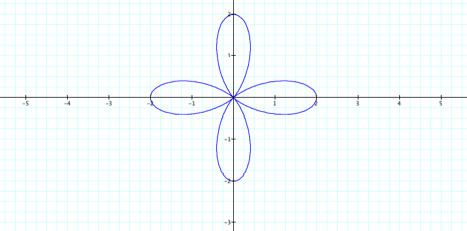
Notice that the value of k, although even, now corresponds to the number of petals? What if k were odd in this same situation?

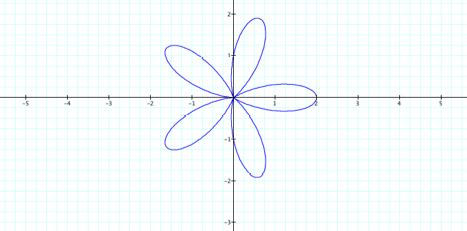
The result appears to hold.

3. What happens if we hold k and b constant and vary the values of a? Consider….

When a is greater than 1, the figure appears to stretch.

Notice that if a is less than one an interesting situation develops.

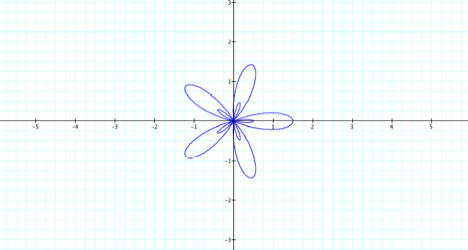
To see an animation of the values of a changing, go here. (Be patient!)

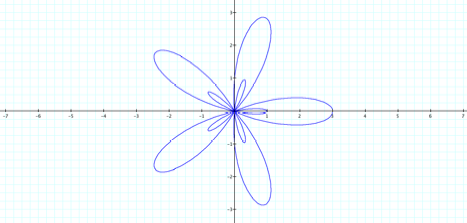
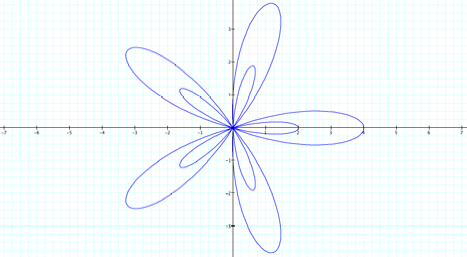
4. What happens if we hold k and a constant and vary the values of b? Consider….

Note that the petal number is the same and appears to be dictated by the value of k and again there appears to be a flower within a flower. If the value of b increases, so does the size of the figure.

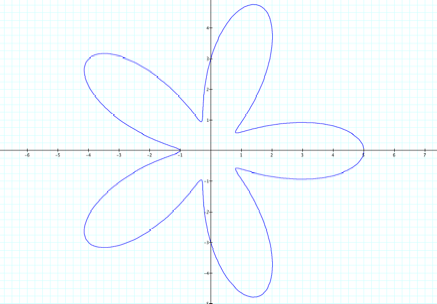
5. What if the value of a is greater than the value of b?

The inside figure disappears and the figure expands.

Part Three

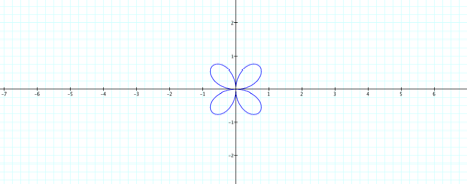
Would any of these patterns hold for sine? Let’s look at one…. Consider….

So if k =2, there should be four petals based on our previous work.

It worked! So if k = 5, there should be five petals….

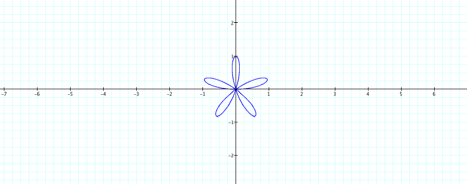
It appears then that some of the basic patterns are the same for sine and cosine in polar equations!

Return