
Proving the Concurrency
of the Perpendicular Bisectors of a Triangle
By Sharon K. OŐKelley
LetŐs
prove that the three perpendicular bisectors of the sides of a triangle are
concurrent which means that they intersect at one point.
To
do so, letŐs consider triangle ABC as constructed in Figure 1. In triangle ABC,
perpendicular bisectors FD and FE have been constructed. If a line is a
perpendicular bisector of the side of a triangle, then it bisects the side into
two halves and forms right angles with the side. Therefore, the following can
be determined from the figureÉ
AD = DC and AE = EB
Angles FDA, FDC, FEA and FEB
are each 90 degrees.
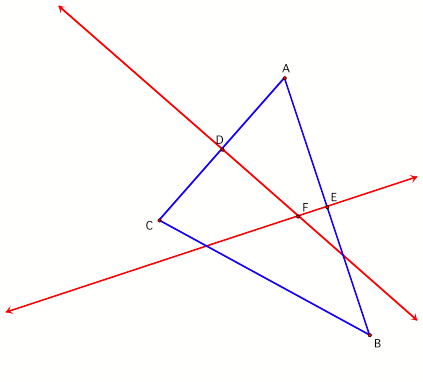
Figure 1
Note
that in Figure 1, perpendicular bisectors FD and FE intersect at point F. To
prove that the three perpendicular bisectors of triangle ABC are concurrent, we
must show that the third perpendicular bisector goes through point F as well.
For
purposes of convenience, perpendicular bisectors DF and FE have been shortened
to segments FD and FE in Figure 2.
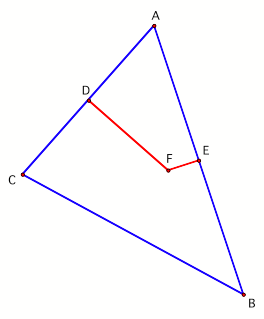
Figure 2
The
Perpendicular Bisector Theorem states that if a point lies on the perpendicular
bisector of a segment, it is equidistant from the endpoints of the bisected
segment.
Hence,
as Figure 3 shows, since point F lies on perpendicular bisector FD, point F is
equidistant from points A and C; therefore, FA = FC. Since point F also lies on
perpendicular bisector FE, it is also equidistant from points A and B;
therefore, FA = FB. Using substitution, it can be concluded that FA = FB = FC.
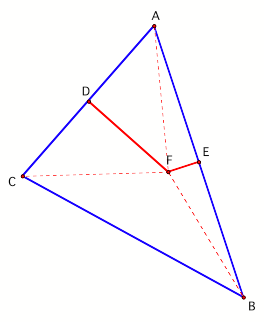
Figure 3
Since
FC = FB, this means that point F must be equidistant from points C and B as
well. Since points C and B are the endpoints of segment BC and point F is
equidistant from those points, it can be concluded that point F lies on the
perpendicular bisector of side BC. That perpendicular bisector has been
constructed as segment FG in Figure 4.
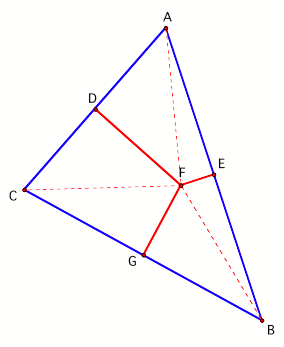
Figure 4
It
can be concluded then that all three perpendicular bisectors, FD, FE, and FG,
are concurrent at point F because point F is equidistant from all three vertices
of the triangle. This point is also called the circumcenter because it is the center of
the circle that circumscribes the triangle. In figure 5, the radii of the
circle are FA, FB, and FC.
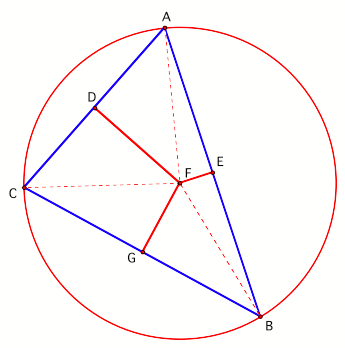
Figure 5