Altitudes and the Orthocenter
By Sharon K. OÕKelley
The Problem
Given
triangle ABC. Construct the Orthocenter H. Let points D, E, and F be the feet of
the perpendiculars from A, B, and C respectfully.
Prove É.
ProveÉ.
Proof 1
Prove É.
Since
there are three different altitudes or height with three different
corresponding bases, the area of triangle ABC can be expressed in three waysÉ.
Note that
within triangle ABC there are three smaller triangles – i.e., 
, 
, and 
The areas of
these triangles areÉ.
The
areas of the smaller triangles and of triangle ABC can now be expressed as
ratiosÉ.
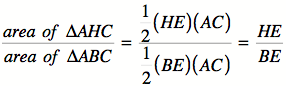
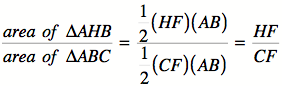
Consider
that the three smaller triangles comprise triangle ABC; therefore, the sum of
their areas will equal the area of triangle ABC. This fact allows for the
following equationÉ.
This
equation can be manipulated to produceÉ.
Using
substitution, the desired result is obtainedÉ.
Q.E.D.
Proof 2
ProveÉ.
Consider
the result from Proof 1 thatÉ.
In
triangle ABC, segments AH, BH, and CH are parts of their respective altitudes;
therefore, they can be used to express the above equation using a variation of
the segment addition postulateÉ.
This
equation can now be rewritten asÉ.
This
can now be manipulated to obtain the desired resultÉ.
Q.E.D.
What if the Given Triangle
is Obtuse? Will These Two Results Hold?
It
was demonstrated in Proof 1 that when triangle ABC is acute thatÉ.
It
follows then thatÉ.
This
also makes sense because segment HE is a part of segment BE; therefore, it is
less than the whole.
Now
consider when triangle ABC is obtuse and the orthocenter is outside the
triangle as shown in the diagram below.
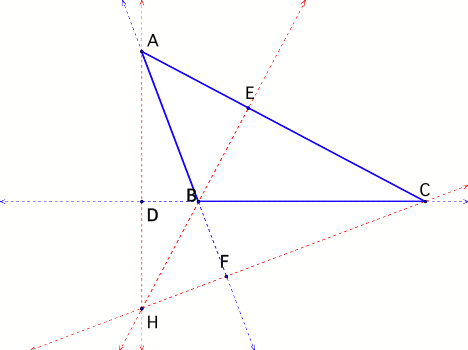
Now
segment BE is a part of segment HE thereforeÉ.
This
would mean thatÉ.
Thus,
the results from Proof 1 and thereby Proof 2 do not hold for the obtuse case.