By Felicia Thrash

 

First, let’s discuss and find out exactly what a stellation is. Stellation is the process of constructing polyhedron by extending the face planes past the edges until they intersect. For example, if you extend the edges of a polygon, they intersect to form a star. In the left diagram below, an 11-sided polygon has its edges extended to form star polygons. Each possible star is denoted by a different color. Beyond the outermost star, all the lines diverge, and never intersect again. Likewise, we can extend the faces and edges of a polyhedron. If we do this to a dodecahedron, as shown at right, the faces become stars and we obtain the star polyhedron shown. This process is called stellation.

 

 

 

 

 

 

More about Stellations

 

You may ask, “Does every polyhedron have a stellation?” Well let’s find out.

In the figure below the edges of the cube and tetrahedron, once extended, never meet. Therefore, these solids have no stellations.

 

 

 

 

If the angle between two faces is greater than 90° there are several layers of bounded cells which may be assembled to build new polyhedra.

 

Octahedron

 

The only stellation of the octahedron is Kepler's Stella Octangula, which is also a compound of two tetrahedra.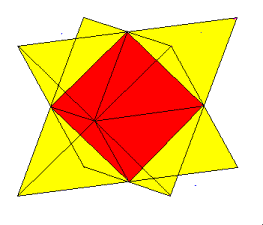

 

Rhombic Dodecahedron

 

The rhombic dodecahedron has only 3 stellations.

 

 

Rhombic Dodecahedron

 

 1^st Stellation of the Rhombic Dodecahedron

 

 

2^nd Stellation of the Rhombic Dodecahedron

 

 

3^rd and Final Stellation of the Rhombic Dodecahedron

 

 

 

 

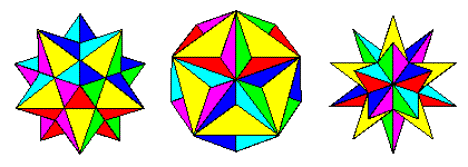
Icosahedron

 

 Here is view of the astounding 59 stellations of the icosahedron.

 

 

 

Now that you have been presented with a little background information on stellations, let’s finally take a look at the stellations of a dodecahedron.

 

 

Dodecahedron

 

  

Here we see a dodecahedron face (blue) with the intersections of all other faces indicated. This is a common way to show the possible stellations of a solid. We see that there are three distinct groups of cells.

 

 

 

 

The three stellations of the dodecahedron are non-convex regular polyhedra and are shown above. The first is the small stellated dodecahedron. The small stellated dodecahedron is formed by placing 12 congruent pyramids on the faces of the dodecahedron. Next is the great dodecahedron.. This is obtained by continuing the star planes of the small stellated dodecahedron outward until they meet to form the next set of pentagons.  These continuations form 30 wedges on the small stellated dodecahedron. If we extend these pentagons, we get the stellation on the right, the great stellated dodecahedron.  These extensions shape 20 spikes onto the great dodecahedron to form the great stellated dodecahedron. Notice that the great stellated dodecahedron has the same number of vertices and vertex arrangement as the dodecahedron.

 

 

 

 

v  Kepler-Poinsot solids

v  History

v  Stellations of dodecahedron in art and culture

v  Duality

v  References