

Exploring Sequences
by
Molade Osibodu
Objective: To use Excel spreadsheets in exploring sequences
Let's begin by exploring the sequence that occurs when the first term in the sequence f(0) = 1, the second term f(1) = 1 and the following terms genereated by adding the previous two terms together. In other words, f(n) = f(n-1) + f(n-2). The sequence is shown in table 1 below.
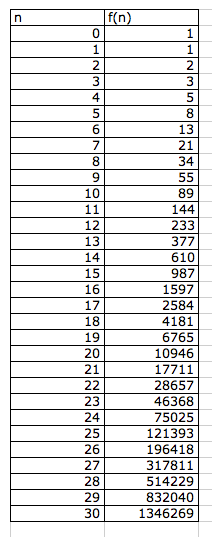
Table 1: Fibonacci sequence
The numbers in f(n) are known as the fibonacci numbers (or sequence) which stems from the rabit problem found in chapter XII in the Liber Abaci book written by Leaonardo of Pisa (1170-1250). In table 1, we see that as n increases, f(n) rapidly increases.
Let's further investigate what happens when we get the ratio of two successive terms. Table 2 shows the result.
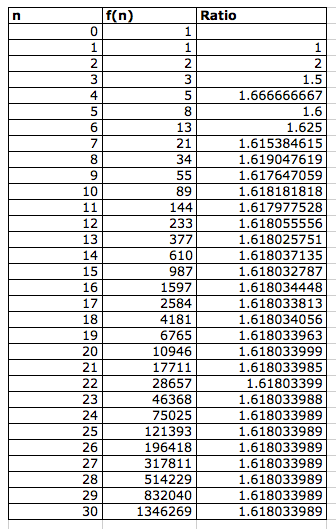
Table 2: Fibonnaci sequence with ratio included
The ratio converges to 1.61803399 which is commonly referred to as the "Golden Ratio". The golden ratio is a very important number that is used to measure beauty and seen in multiple patterns.
Now, let us investigate the case where f(0) = 1 and f(1) = 3
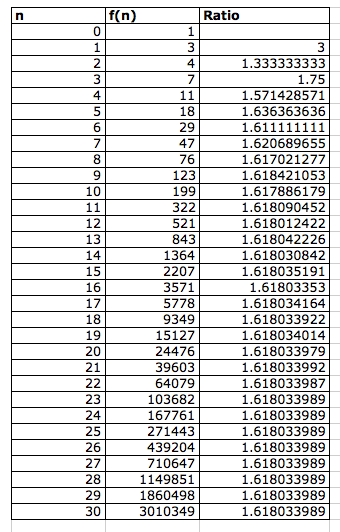
Table 3: Sequence with f(0)=1 and f(1) = 3
In this case, as n gets bigger, f(n) increases more rapidly than in the previous case. The ratio of each successive term still converges to the golden ratio. In fact, no matter what number you use for f(0) and f(1), it would always converge to the golden ratio. Click here and change the f(0) and f(1) term to prove this conjecture.
A special case similar to the fibonacci sequence is known as the "Lucas numbers". The sequence was named after Francois Edouard Anatole Lucas (1842-1891). The difference between the lucas numbers and fibonacci numbers is that f(0) = 2 and f(1) = 1 as opposed to f(0) = 1 and f(1) =1.
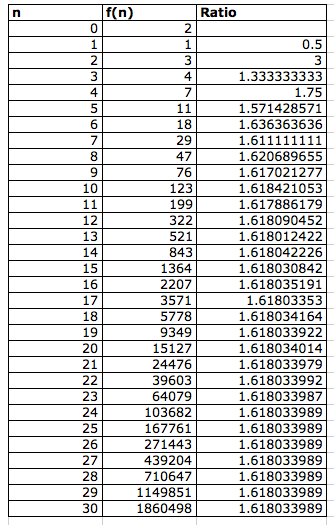
Table 4: Lucas numbers
What happens when f(0 )= 0, f(1) = 1, and f(n) = f(n-1) + 2*f(n-2)
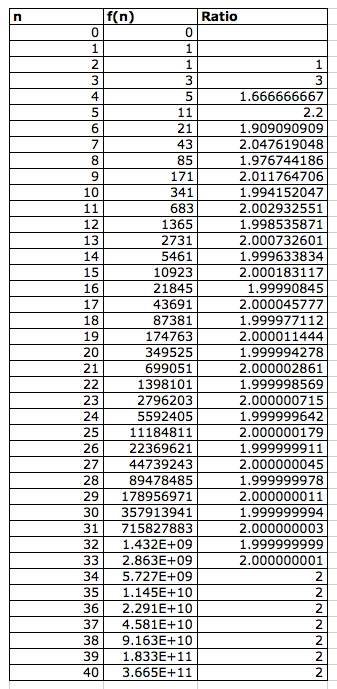
Table 5: Jacobsthal number
This sequence is termed the Jacobsthal number, named after Ernst Jacobsthal. The ratio of this numbers converge to 2. We can create the Jacobsthal-Lucas numbers by letting f(0) = 2 and f(1) = 1.
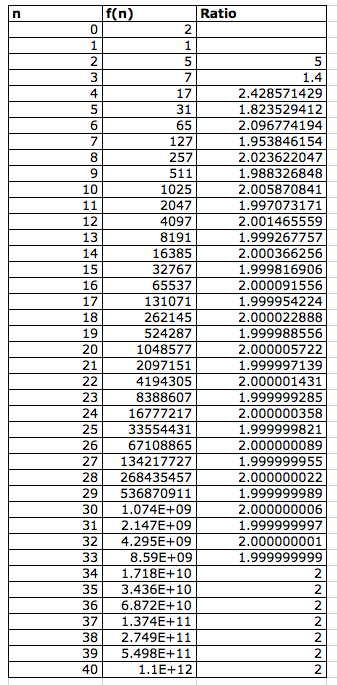
Table 6: Jacobsthal-Lucas numbers
Although the terms in f(n) vary, the ratio of successive terms still converge to 2. Click here and change the f(0) and f(1) term to prove this conjecture.
Note that changing the ratio to be every third term doubles the number it converges to. The fibonacci sequence converges to 2.610339989 (click here) while the jacobsthal sequence (click here) converges to 4.
In summary, spreadsheets can be used for a VARIETY of investigations. They are especially useful in viewing patterns and sequences generated from a set of numbers. They are also useful is suggesting that sequences converge but a proof should be given to confirm the observation.