
Assignment 8 :: Altitudes and Orthocenters
By Jamie K.York
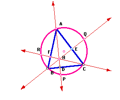
The altitude, or height, of a triangle is a component and measurement that is taught very early in mathematics, as it is an essential part of calculating area, A = 1/2 bh. Constructing the altitude from each side of a given triangle gives us what we refer to as the orthocenter, the intersection of the three altitudes. Below is an example using a given triangle ABC.
To further our investigation of triangles and orthocenters, continue with the steps below:
1. Construct any triangle ABC.
2. Construct the Orthocenter H of triangle ABC.
3. Construct the Orthocenter of triangle HBC.
4. Construct the Orthocenter of triangle HAB.
5. Construct the Orthocenter of triangle HAC.
6. Construct the Circumcircles of triangles ABC, HBC, HAB, and HAC.
The resulting image should appear similar to the one below.
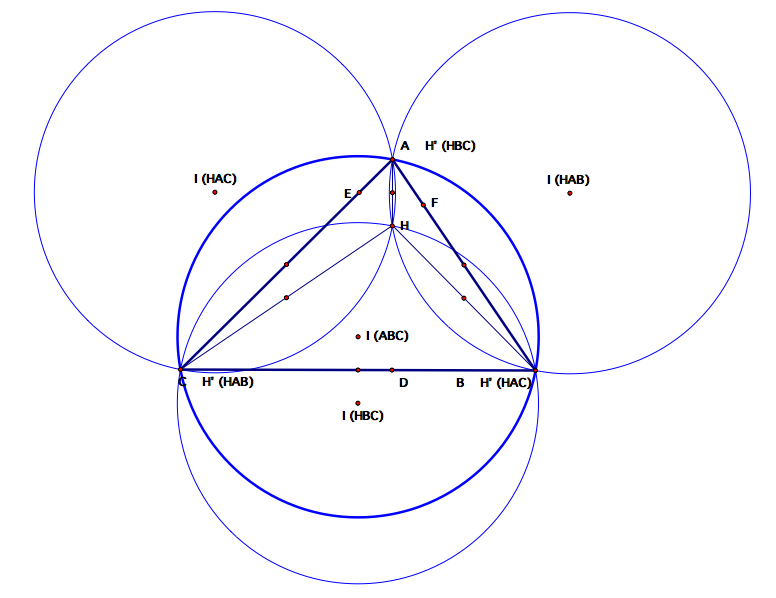
Notice that in locating the orthocenters of the three triangles formed with point H
aren't new points, but they are in fact vertices of the original triangle ABC.
As we consider the midpoints of the segments of each triangle, we begin to see
the formation of the nine point circle that we worked on in assignment
4. We can complete the nine point circle in this example in the same manner
as we did in assignment 4 (see below).
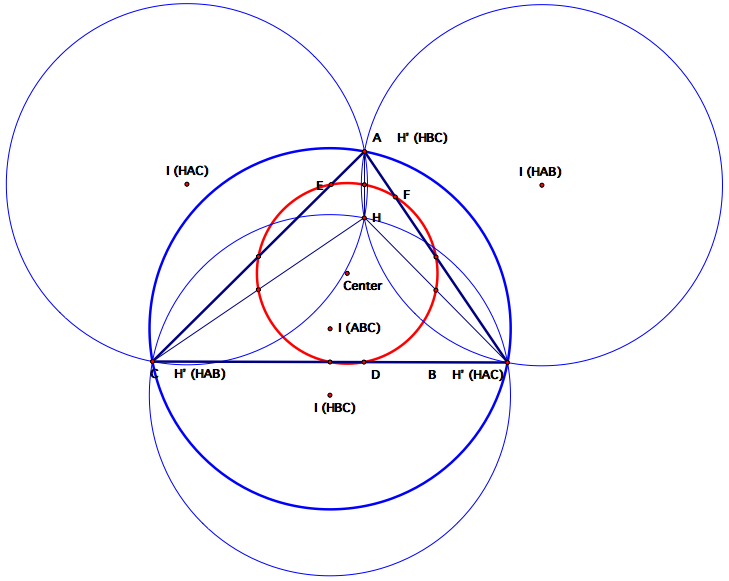
Use the GSP file to further investigate different types of triangles
and the resulting configuration. Specifically compare and contrast actue, right, and obtuse triangles.
In assignment 5 we created a script tool that can be used to find the orthocenter of any given triangle. Use this tool to furthe investigate the concepts of altitudes and orthocenters.
Orthocenter Script Tool (GSP file)
Home | EMAT 6680
| Dr. Jim Wilson