By: Erica Fletcher

In this assignment we will explore rational functions and the properties of their graphs such as domain, vertical and horizontal asymptotes, x and y intercepts.

Consider rational equations of the form:

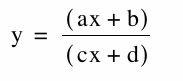
We will first explore what happens to the vertical and horizontal asymptotes as we change the variables a, b, c, and d.

Recall that an asymptote of a curve is a way of describing its behavior far away from the origin by comparing it to another curve. Asymptotes occur when you have a value for which the particular function being studied is undefined, and where the limit is either positive or negative infinity.

 

We will start this exploration using generic values of a = 1, b = 2, c = 3, and d = 4 as follows. Look at the graph below:

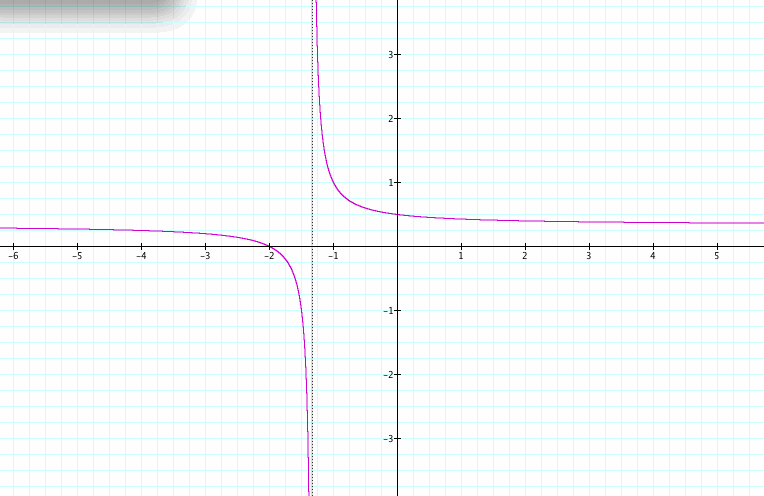
Now let's look at what happens when a = 4, b = 3, c = 2, d = 1.

 

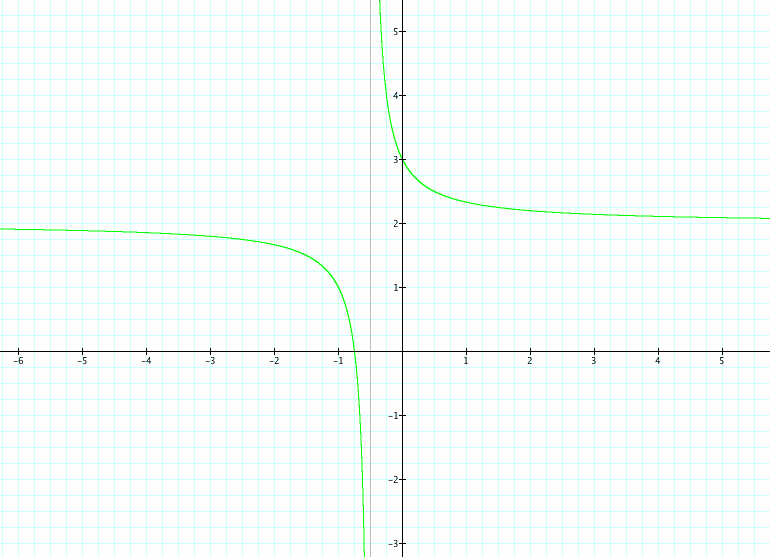
Rational functions are very interesting equations to explore. So let's keep going.

Now let's look at what happens when a is positive but b, c, and d are negative.

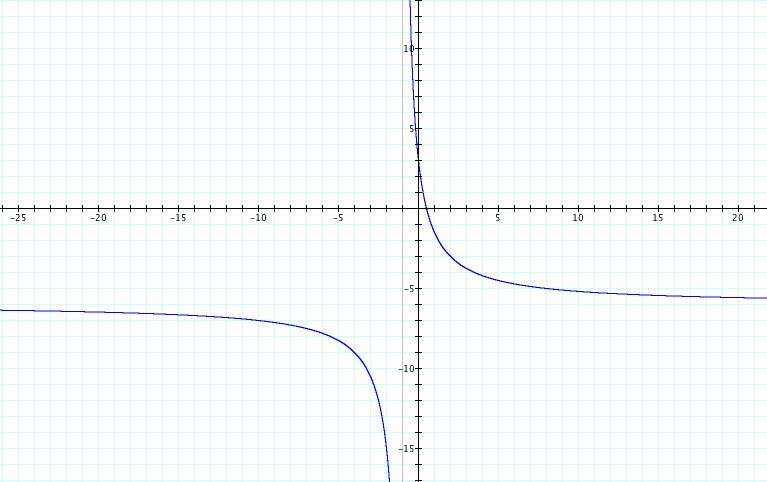
Conversely, let's look at what happens as a is negative.

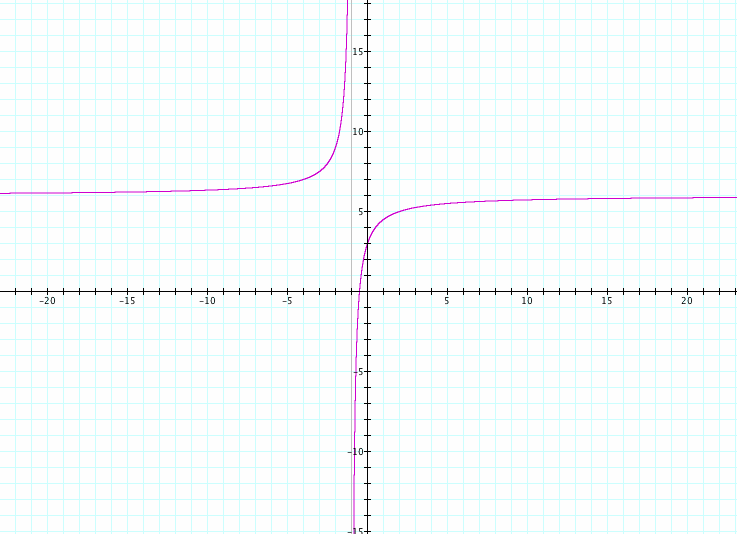
As a changes we notice a couple of different things happening:

Let's see now how changing the variable b affects the graph.

Observe what happens when b is positive.

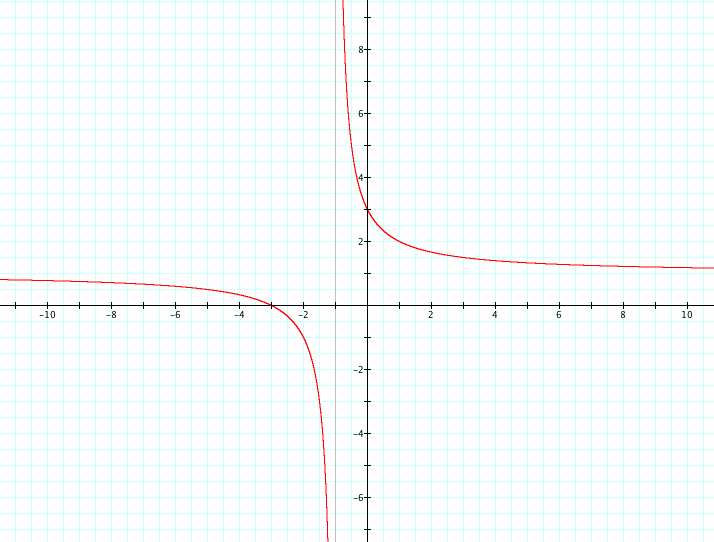
Now let's see what happens when b is negative while keeping the other variables positive.

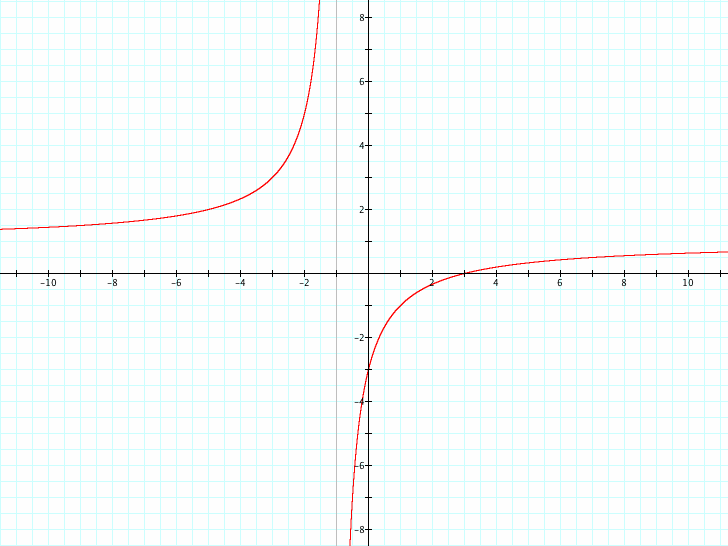
As "b" changes we notice that the asymptotes are the same as "a" but the graphs are slightly different where y = b.

Let's explore further.

We wonder what happens when we change "c". How will the graph be affected?

Let's first see what happens when c is positive.

Check out this video when c varies from 0 to 10 (stays positive).

Now let's see what happens when c is negative.

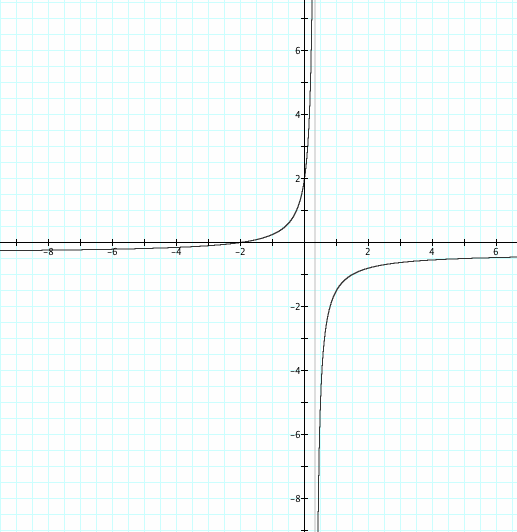
Check out this video to explore what happens as "c" is negative.

We notice that as "c" changes the vertical asymptote is now at x = -1/c.

Last but definitely not least, let's explore what happens when we change "d".

How is the graph affected when d is positive?

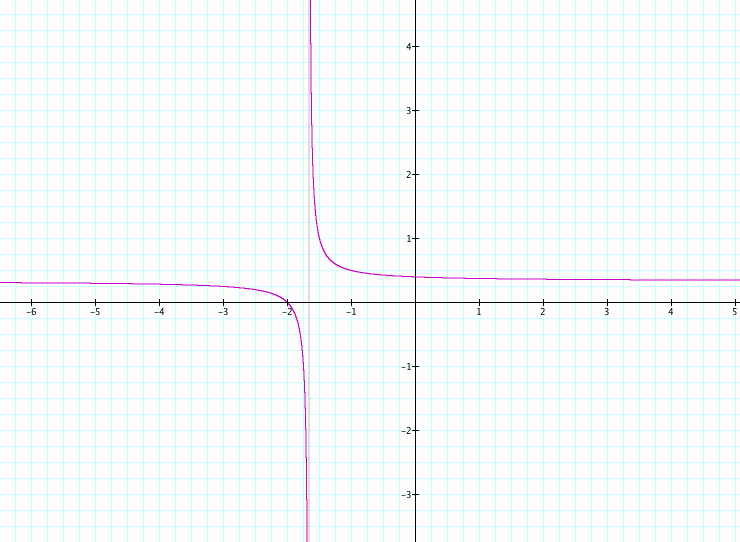
How is the graph affected when d is negative?

 

 

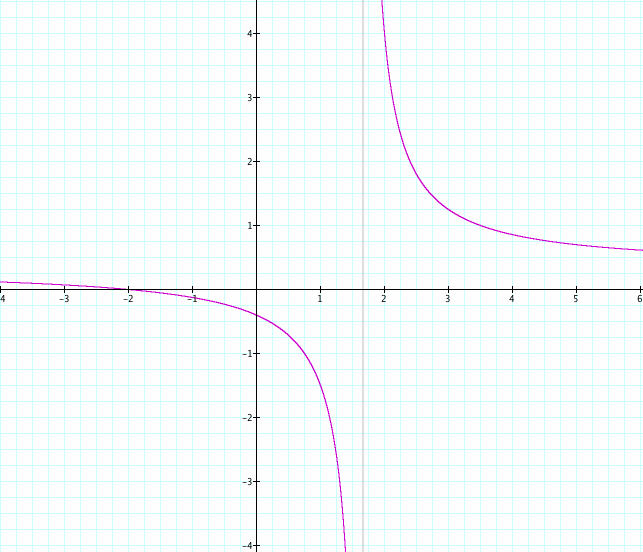
Check out this video to see what happens when we have the following range -10 < d < -10.

As "d" changes we notice that the vertical asymptote is now at x = d.

As we look at several different equations while varying the variables a, b, c, and d we see some interesting math.

In general, as all values approach zero the two parts of the graphs converge upon one another. As the values distance themselves from zero, the two parts move further away from one another.

If you look at all of the graphs above and explore with the videos you will see different things happening to the roots of the rational equation:

.

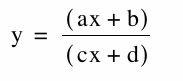Recall: A root or x- intercept occurs when our function crosses the x - axis. Algebraically we have:

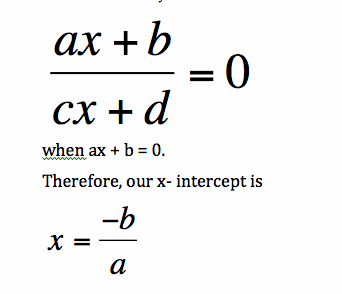
As we look for our y-intercepts in the graphs above we notice that its always b/d as long as d does not equal zero.

Let's explore further.

What happens to our graph when a = b = c = d = 1.

When a = b = c = d = 1, the graph appears to be continuous. However, there is a hole at f (-1) and that is because the rational equation above is undefined. Also we notice ad - bc = 0 so the graph will always result in a horizontal line when a = b = c = d.

What happens when we see holes in our graph? After observing what happens everytime a = b = c = d (negative and positive values excluding 0), we notice that where x = -d/c there is a hole in our graph. If  you would like to explore this conjecture further think about limits. It is important to remember that a limit can also exist if a function is continuous.

Now let's explore what happens as we look at the numerator and denominator alone of the following function:

.

 

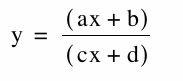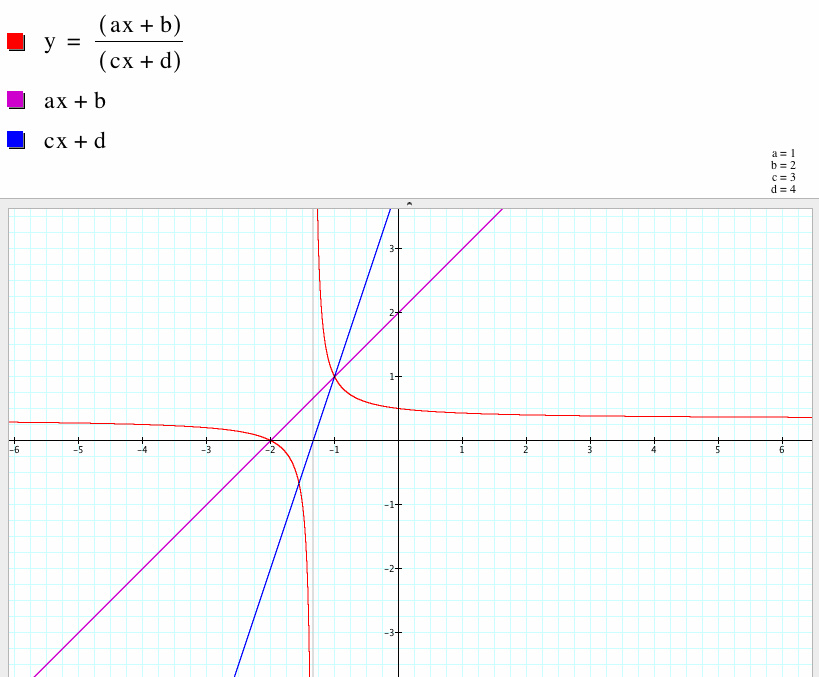
One observation is that the y-intercepts of the numerator and of the original rational equation are the same. This happens when the numerator equals 0. Now one may wonder what happens when the denominator equals 0. We notice that the graph has a vertical asymptote. This makes sense because it is IMPOSSIBLE to divide by 0.

If you have time, you should explore what happens when you create an animation using graphing calculator as a, b, and d change together and leave c the same.

 

 

Return to Fletcher's Home Page