Tangent Circles

by Hwa Young Lee

When given two circles of different size, how many possible cases are there in positioning the two circles on the same plane?

We can think of five distinct cases:

1) One given circle lies completely inside the other.
2) The two given circles intersect at two distinct points.
3) The two given circles are apart and disjoint.
Five possible positions of two circles on the same plane
4a) The two given circles are tangent, in the inside.
4b) The two given circles are tangent, in the outside.

Here, we are going to construct a circle tangent to the two circles with one point of tangency being the designated point for cases 1), 2), and 3).

For each case, we are going to investigate the loci of the centers of the constructed tangent circles.

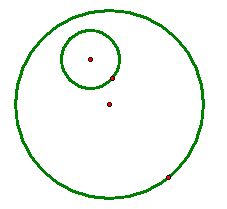
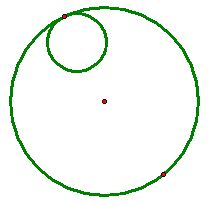
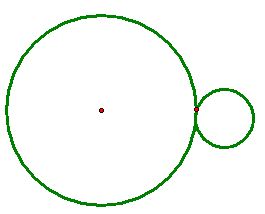
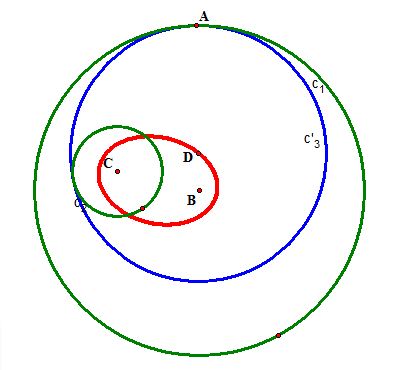
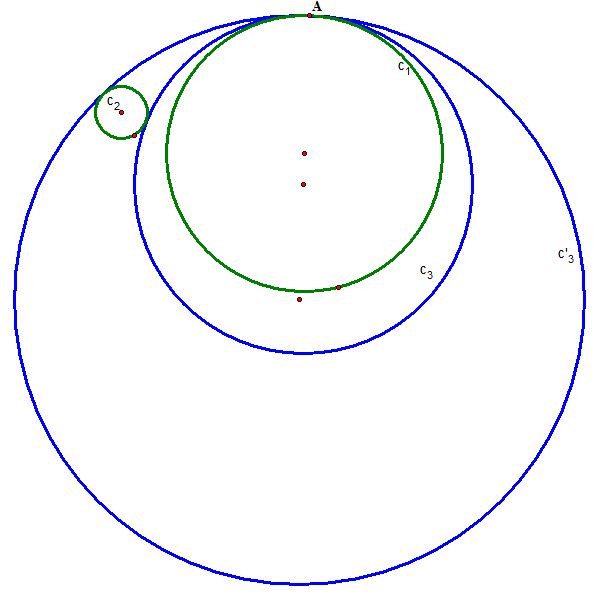
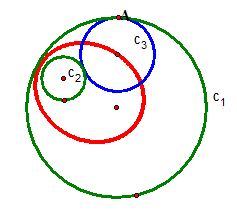
Case 1) When one given circle lies completely inside the other:

First, let's construct a circle tangent to the two circles and with one designated point A of tangency on .

We want to find the circle that passes point A with it's center equidistance from point A and some point on .

We know that the center is going to be somewhere on the line l which connects the center of and A.

However, since we do not know where that some point on will be, we use the center of the circle.

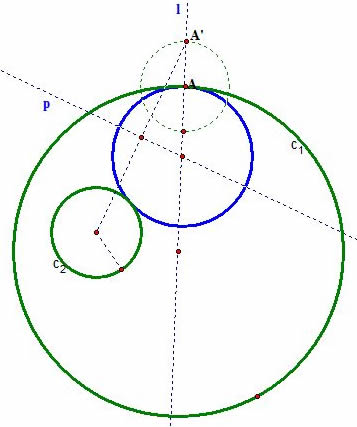
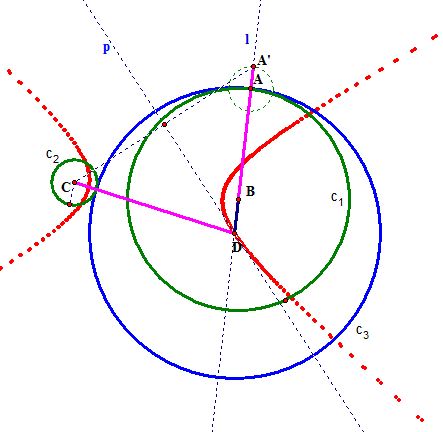
So, we extend point A along line l by the length of the radius of the small circle and mark point A'.

To find a point on line l that is equidistance from the center of to point A', we use the fact that the points equidistance from two points are on the perpendicular bisector p of the segment connecting the two points.

Now, we find the intersection of line l and  line p which is the center of our desired circle, and construct our circle (in blue)!

 

Now, let's investigate the locus of the center of . Let's first examine this by tracing the center of the circle as point A moves along the larger circle. You can explore this in a GSP animation of this. Try moving around inside and examine the locus.

What does the red trace of center look like? We conjecture that the locus of the center of the tangent circle is an ellipse.

To confirm, we provide a justification. Let's go back to our construction of .

From our construction, we know that .

Meanwhile, we know that the length of   is the sum of the radii of and .

Now, since we know that ,

.

So, as point A moves along , the position of point D might change but is constant.

This means that the sum of distance from point D to two fixed points C and B is constant.

Hence, points B and C are the foci of an ellipse, which is the locus of the center of .

 

 

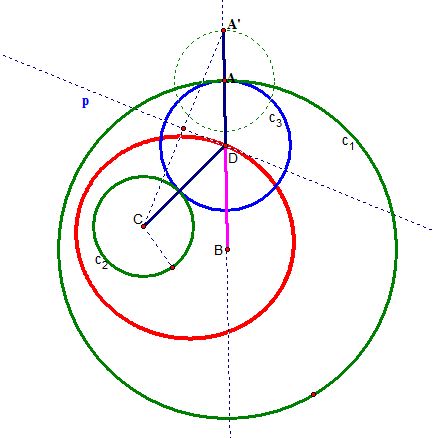
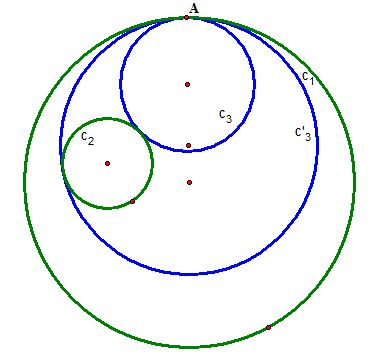
However, we are missing something in case 1). Can you notice what that is? is not the only possible tangent circle.

Yes, we can construct a tangent circle that contains . This time, we want to find a point on line l that is equidistance from a point on , but on the opposite side of the center.

Thus we move point A along line l by the length of the radius of and mark point A''.

Like we did earlier, we use the perpendicular line from the midpoint of the two points A'' and C.

By this, we obtain our center D and construct our tangent circle !

 

 

 

 

 

 

Let's take a look at the locus of the center of this tangent circle. Let's first examine this by tracing the center of as point A moves along . You can explore this in a GSP animation of this. What does the red trace of center look like?

We conjecture that the locus of the center of the tangent circle is an ellipse.

To confirm, we provide a justification.

From our construction, we know that .

Meanwhile, we know that the length of is the difference of the radii of and .

Now, since we know that ,

So, as point A moves along , the position of point D might change but is constant.

This means that the sum of distance from point D to two fixed points C and B is constant.

Hence, points B and C are the foci of an ellipse, which is the locus of the center of .

 

 

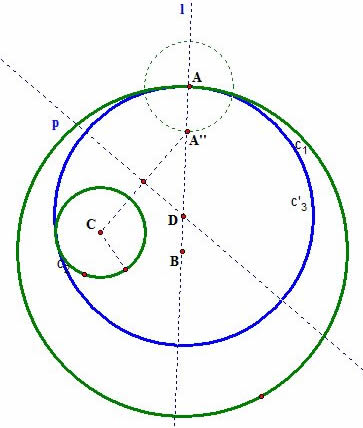
To sum up, in case 1), we can construct two tangent circles and :

For a GSP script tool for this construction, click here.

and the loci of the center of the two tangent circles and form ellipses with the same focal points:

For a GSP animation of the two tangent circles and ellipses, open this GSP file and press the animation button.

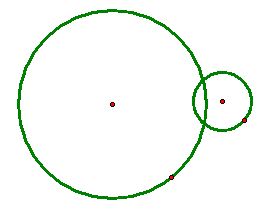
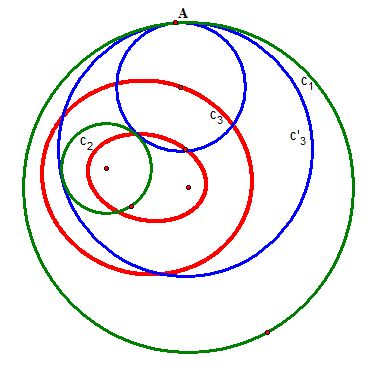
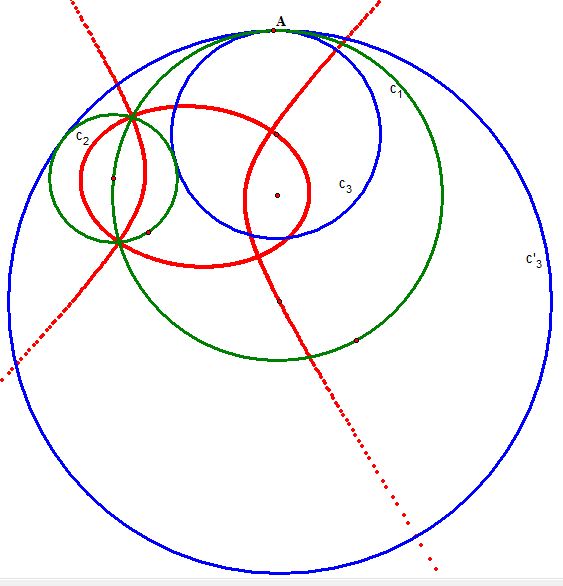
Case 2) When the two circles and overlap and thus intersect at two distinct points:

Since we carefully constructed the tangent circles in case 1), we can easily find the tangent circles by moving the position of  so that it satisfies our second case.

For a GSP script tool for this construction, click here.

That was pretty easy. This is why "constructing" is important and useful compared to "drawing" a figure. If you construct an object, it means that when the figure is moved around, the features of the object do not change; only the size or position might change, while still remaining the object as desired.

Now, since we have our tangent circles, do you think the loci of the centers of the tangent circles are still ellipses? Let's first examine this by tracing the centers as point A moves along . You can explore this in a GSP animation of this. 

We conjecture that the locus of the center of the smaller tangent circle (internally tangent) is an ellipse

and the locus of the center of the larger tangent circle (externally tangent) is a hyperbola.

To confirm, we provide a justification.

Let's start with .

From our construction, we know that .

Meanwhile, we know that the length of is the sum of the radii of and .

Now, since we know that ,

So, as point A moves along , the position of point D might change but is constant.

This means that the sum of distance from point D to two fixed points C and B is constant.

Hence, points B and C are the focal points of an ellipse, which is the locus of the center of .

 

 

 

Let's go on to .

In this case, the situation is a little different.

Here, we know that , from our construction.

But in this case, and thus

Meanwhile, we know that the length of is the difference of the radii of and .

Thus shows us that the difference of distance from point D to two fixed points C and B is constant.

Hence, points B and C are the foci of a hyperbola, which is the locus of the center of .

 

 

To sum up, in case 2), we can construct two tangent circles, one internally and one externally tangent. The loci of the center of the internally tangent circle is an ellipse and the loci of the center of the externally tangent circle is a hyperbola. The ellipse and the hyperbola formed have the same focal points.

For a GSP animation, click here.

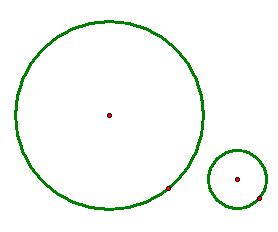
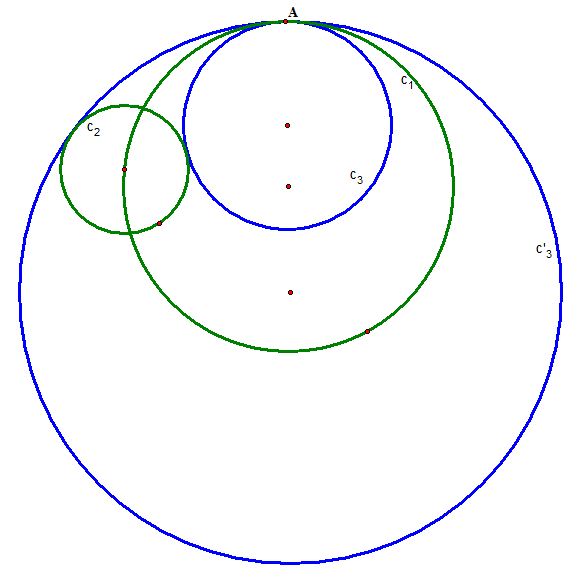
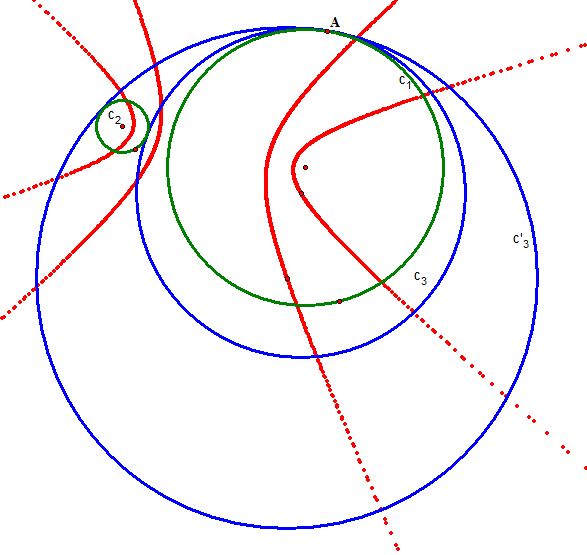
Case 3) When the two circles and are apart and disjoint:

Since we carefully constructed the tangent circles in case 1), we can easily find the tangent circles by moving the position of  so that it satisfies our third condition:

What would the loci of the centers of the tangent circles be? Let's first examine this by tracing the centers as point A moves along .

You can explore this in a GSP animation of this.

We conjecture that the loci of the center of the two tangent circles form hyperbolas with the same focal points.

To confirm, we provide a justification. Let's start with .

From our construction, we know that .

Meanwhile, we know that the length of  is the sum of the radii of and .

Now, since we know that ,

So, as point A moves along , the position of point D might change, but  is constant.

This means that the difference of distance from point D to two fixed points C and B is constant.

Hence, points B and C are the focal points of a hyperbola, which is the locus of the center of .

 

 

 

Let's go on to .

Here, we know that , from our construction.

But in this case, and thus

Meanwhile, we know that the length of  is the difference of the radii of and .

Thus shows us that the difference of distance from point D to two fixed points C and B is constant.

Hence, points B and C are the foci of a hyperbola, which is the locus of the center of .

 

 

To sum up, in case 3), we can construct two tangent circles, one internally and one externally tangent.

For a GSP script tool for this construction, click here.

The loci of the centers of the two tangent circles both form a hyperbola of  the same focal points.

For a GSP animation, click here.