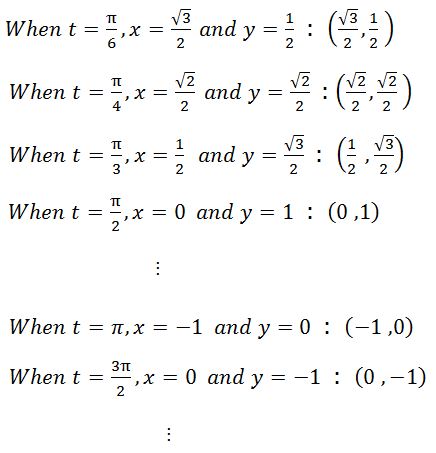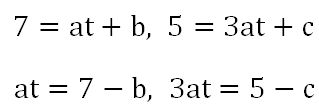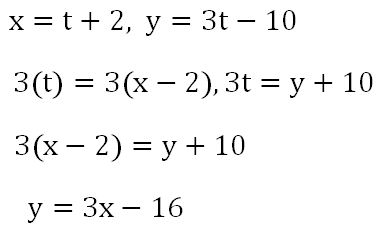Parametric Equations
by Hwa Young Lee
In this assignment, we are going to investigate parametric equations and parametric curves through four examples.
Let's start with an example to get an idea of what parametric equations and parametric curves are.
Example 1) I wanted to keep track of the motion of a car while it was continuously moving, as time passes, for 10 minutes. Strangely, I only had a device that kept track of the movement of the car horizontally or vertically.
So, I observed the horizontal movement of the car and found that the car was continuously moving east such that the horizontal position of the car at t minutes was
x(t)=2t
The vertical movement of the car turned out to be continuously northbound, with a vertical position at t minutes expressed as
y(t)=t+3
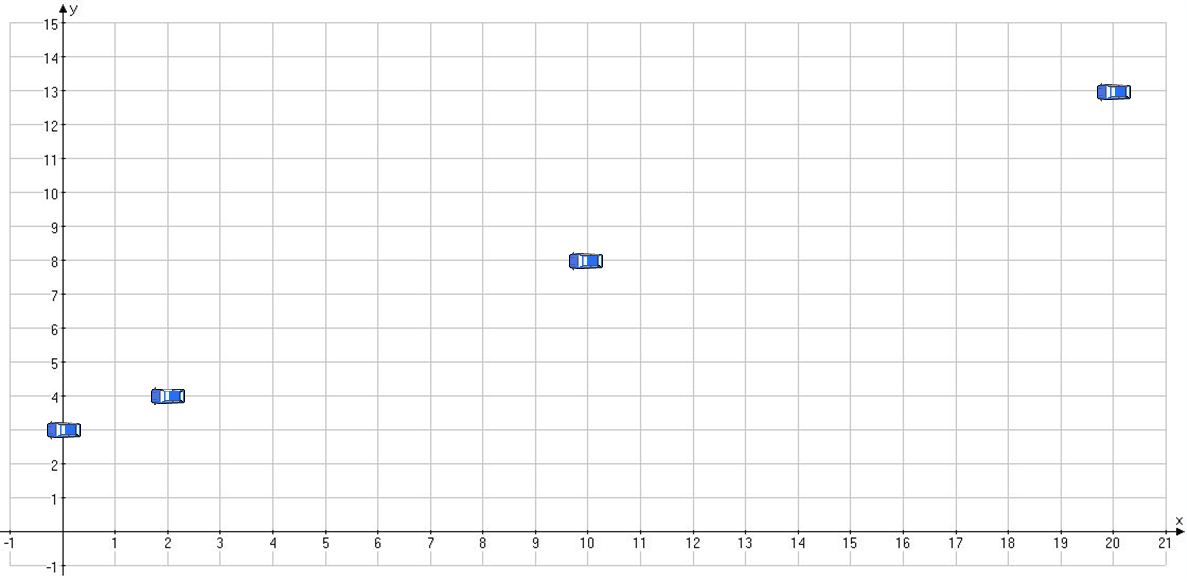
To find out how the car is moving in whole, I plotted the car on the xy-coordinate. Since we are looking at
, let's find out a few points within that range.
When t=0, then x=0 and y=3 so the car is at (0, 3), the initial point.
When t=1, then x=2 and y=4 so the car is at (2, 4).
When t=5, then x=10 and y=8 so the car is at (5, 8).
When t=10, then x= 20 and y=13 so the car is at (20, 13), the terminal point.
We obtain a few points as the following graph:
But these are only a few points that show the movement of the car.
What would the general (since we know the car is moving continuously in its manner) movement of the car?
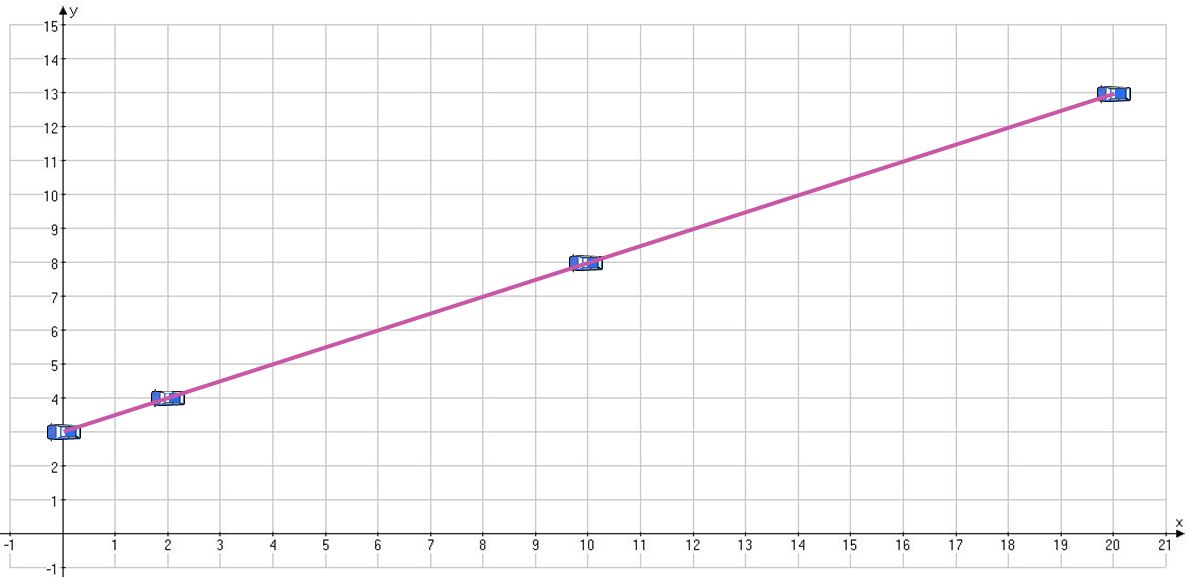
From x=2t and y=t+3, we can find a relationship between x and y by eliminating the parameter t.
Since t=y-3 if we plug this in the first equation, we obtain x=2(y-3) and rearranging this in terms of y, we see that
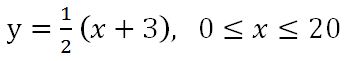
is the function that shows us the movement of the car. Here, we know that the domain is derived due to the range of t. Hence, we confirm that the movement of the car is along the pink line in the figure below, with a direction (north-east bound).
From this example, we saw that in a function involving two variables x and y, it is possible to express x and y in terms of a third variable.
This third variable is called the parameter, usually denoted as "t".
For the two continuous functions x=f(t), y=g(t), substituting values for the parameter t results in ordered pairs (x, y), which form the points on the parametric curve.
We call x=f(t), y=g(t) the parametric equations of the parametric curve.
Plotting the points as t increases gives the parametric curve a direction and also the range of t is important in graphing the curve.
Since we are plotting the points as t moves on the xy-coordinate plane, by finding an equation in terms of x and y by eliminating the parameter, we can graph the parametric equations. However, since the range of t is important, when eliminating the parameter, it is important to check the domain!
Let's take a look at another example.
Example 2) Janet was lazy laying in bed and was watching the ceiling when she discovered a fly was flying in a strange movement (Does this situation remind you of something? Yes, this is how Descartes first invented the Cartesian plane). She wanted to find out the actual movement of the fly and used a device that gives the horizontal and vertical position at t radians: the parameter for this case would be the angle t of the rotation. As a result, she obtained
Can you plot the movement of the fly on the xy-plane? In other words, can you draw the parametric curve of
?
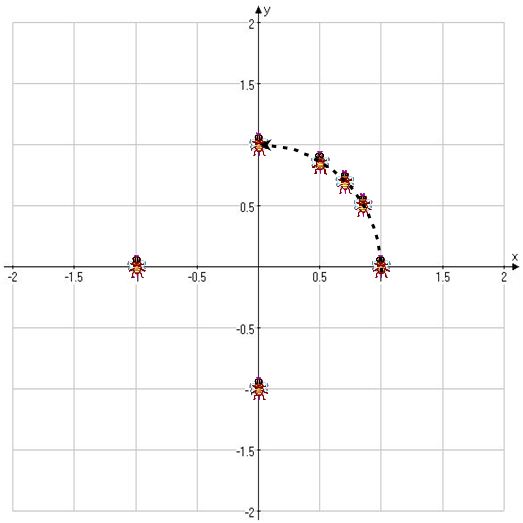
Let's plot a few points on the plane.
When t=0, x=1 and y=0 so the fly is on (1, 0).
But these are only a few points that show the movement of the fly. We can guess that the fly is flying in a circle, but we cannot confirm with just a few points.
However, from
In this case, recall the identity
and by eliminating the t, we obtain
which gives us the unit circle! In this case, since t ranges from 0 to
, we complete the unit circle and the direction of the movement is counterclockwise.
'
So the fly was flying in a circle, counterclockwise!
Actually, in assignment 3, we did something similar to this to find the locus of the vertices of different parabolas as b varies for
. In this case, b was our parameter and by eliminating b, we obtained the parametric curve ( a parabola) with an equation of
.
We found parametric curves for parametric equations. Conversely, can you find parametric equations for a given parametric curve? Try two examples.
Example 3) Write parametric equations of a line segment through (7, 5) with slope of 3.
Since we want to see the movement of the points along the line, we first start with the slope.
Recall from Example 1) that the slope of the parametric curve was
. This was due to the movement of x and y regarding t: x was moving at a rate of 2t while y was moving at a rate of t. So, when x was increasing 1 unit (horizontally), y was increasing
Since the slope of the line segment in this case is 3, this shows us that the points along the line are increasing every 3 units vertically when moving 1 unit horizontally.
This gives us a start with
, for some a, b, and c
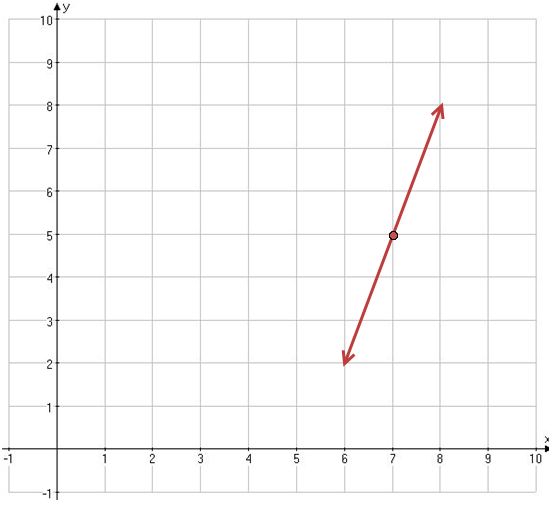
Now, we want this line segment to pass point (7, 5), which means for a particular t value, we want x=7 and y=5.
Hence,
and multiplying the first equation through by 3, we get
Thus, we can we find the parametric equations for the desired line segment:
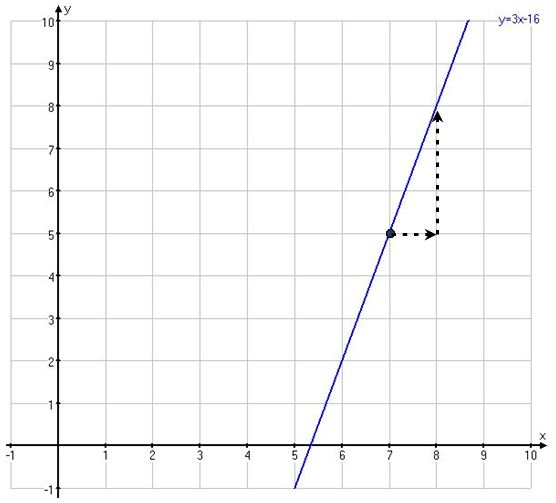
Let's check by picking a=1, b=2, and c=-10. Then
and we can check that the graph of this gives us the desired line segment: by restricting the range of t, we can form various segments.
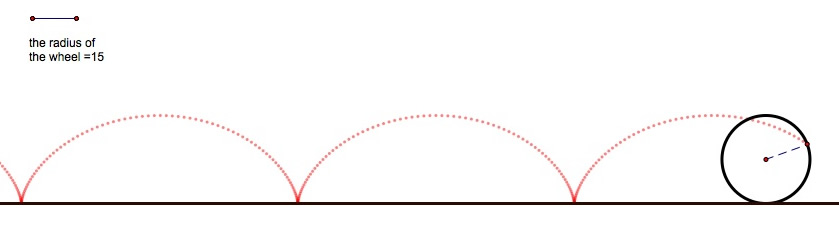
Example 4) Matt discovered a lump of gum stuck to the front tire of his bicycle. He became curious of the movement of the gum as the bike was gliding along the road. Assuming the road is flat, the bike is gliding along a straight line, and the tire is a perfect circle with radius 15 inches, what would the locus of the gum (a fixed point on the circle) be? (click here for a GSP animation)
The locus of a fixed point on a circle rolling along a line is called a cycloid. Now, try finding parametric equations for the cycloid in Matt's case.
The answers are in the final assignment.
