Rational Equations
By Leighton McIntyre
Goal: to show the effect of changing the parameters a,b,c and d in rational equations, and to extend the discussion to various examples of 
Rational equations are equations of the form  , where f(x) and g(x) are polynomials and g(x) is not zero.
, where f(x) and g(x) are polynomials and g(x) is not zero.
One form of rational functions explored in this discussion is 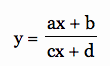
A typical graph of this type of equation looks like the diagram below:

The horizontal asymptotes of this graph is y = 2 because the graph of the equation gets closer and closer to the line y=2 but never touches the line y = 2.
The vertical asymptotes of this graph is x=1 because the graph gets closer and closer to the line x = 1 but never touches the line x = 1. the values of the constants and coefficients of this graph are a = 2, b = 1, c = 1, and d = -1.
In assignment 1, we showed that in general, given a rational function  where f(x) = ax + b and g(x) = cx + d, the horizontal asymptotes occur where the domain of the function breaks, that is where the denominator g(x) is equal to zero. In this case cx + d = 0, thus the vertical asymptote is x = -d/c. The horizontal asymptotes occur where y = a/c because as x gets infinitely large or small then the numerator tends to something extremely large times a or something extremely small times a, while the denominator tends to something extremely large times c or something extremely small times c.
where f(x) = ax + b and g(x) = cx + d, the horizontal asymptotes occur where the domain of the function breaks, that is where the denominator g(x) is equal to zero. In this case cx + d = 0, thus the vertical asymptote is x = -d/c. The horizontal asymptotes occur where y = a/c because as x gets infinitely large or small then the numerator tends to something extremely large times a or something extremely small times a, while the denominator tends to something extremely large times c or something extremely small times c.
In the case of the hyperbola given in the example, we see that the asymptotes are y = 2, a horizontal line, and x = 1, a vertical line. Because the asymptotes consist of a horizontal line and a vertical line, then the lines are perpendicular. A hyperbola which has asymptotes meeting at right angles is called a rectangular hyperbola. In the above example the center of the hyperbola is at (1,2). In general the center of a rectangular hyperbola is at (-d/c, a/c).
Changing the parameter a
Let us look what happens when we change the parameter a
Let us again visualize what happens as parameter a changes.
let b=1, c= 1, d = -1, and a vary in units from a= -2, - 1, 0, 1, 2

There are a few things that we notice from this diagram:
1) All the graphs pass through the point y = -1. This point is the y-intercept of the entire rational equation. The y-intercept is the point where the value of x = 0. Thus in general, the y-intercept is the point (0, b/d)
2) When a = -2, the graph cuts the x-axis at 1/2, and when a = 3, the x-intercept is -1/3. The x- intercept of the functions occur at the point where y = 0. This is the same as setting the numerator equal to zero. Thus the x-intercept of the rational equation is the x-intercept of the numerator. In general, the x-intercept is the point (-b/a, 0). Changes in a causes changes in the x-intercept
3) All the graphs except the one in which a = 0 are hyperbolas, therefore at a = 0, there is a special case for the rational equation.
4) The graphs of the hyperbolas all have a vertical asymptote at x=1. A vertical asymptote occurs where the value of the denominator equals zero. Since in this case the denomination cx + d is x - 1; setting x - 1 = 0 gives the vertical asymptote as x = 1.
5) The graphs of the hyperbolas have different horizontal asymptotes which appear to vary directly with the changes in a. The horizontal asymptote where a = -2 lies at y = -2 and this idea is seen at each value of a. Since from previous knowledge of rational function the y asymptote occurs at y = a/c, we can say that the y asymptote occurs here at the value if a because the value of c is 1, and therefore the value of a/c=a/1 = a. However in general the y asymptote occurs at y = a/c.
6) As we move from left to right along the graph we notice that the graphs flip as you move past the vertical asymptote. The purple graph is always an increasing function, while the green and light blue functions are always decreasing functions. There is a reason fro this which will be explored as we move along with this investigation. It has to do with the difference between ad and bc. Notice that for the purple line ad - bc > 0 and for the green and blue curves ad and bc < 0.
When using the Graphing Calculator software, in order to view the dynamic changes in the parameter a we replace the parameter a in the equation by the parameter n (because this is the parameter that graphing calculator recognizes as one that can easily change values, and let the parameter n take on a number of values from say -10 to 10 and observe what happens in the graph. The graph of this equation looks like this in motion form:
Changing the parameter b
Let us look what happens when we change the parameter b

Notice what happens as the parameter b is changed.
1) The y-intercept changes as the parameter b is changed. When b = 10, the y intercept is at -10, and when b is at -5, the y intercept is at 5. Looking at this pattern one might be tempted to deduce that the y-intercept is the opposite of the value of b in the rational equation. One must be cautious however because there are unit values in the equation. Since the value of d in the equation is -1, we can see that if we divide the value of b by the value of d in each equation this will give the exact value of the y-intercept and thus we can state that the y-intercept is the point (0, b/d)
2) When b = 10, the graph cuts the x-axis at -5, and when b = -5, the x-intercept is 2.5. Again, the x-intercept is the point (-b/a, 0). Changes in b causes changes in the x-intercept.
3) All the graphs except the one in which b = -2 are hyperbolas, therefore at b = -2, there is a special case for the rational equation.
4) The graphs of the hyperbolas all have a vertical asymptote at x = 1.
5) The graphs of the hyperbolas have the same horizontal asymptote at y = 2. The horizontal asymptote as at a/c = 2/1 = 2. Since a/c is the same constant for all the equations, then the horizontal asymptote for all the hyperbolas will be the same.
6) As we move from left to right along the graph we notice that the graphs flip as you move past the vertical asymptote. The light blue graph is always an increasing function, while the purple, red and dark blue functions are always decreasing functions. There is a reason . Notice that for the light blue hyperbola ad - bc > 0 and for the purple, red and dark blue curves ad and bc < 0.
The graph of the changes in b looks like this in motion form:
Notice what happens as the value of b changes from -10 to 10 the point that the graph cuts the y-axis moves from y = -10 to y = 10,The graph changes direction at y = -2. So between b = -10 and b = -2, the graph lies in the second and fourth quadrants of the intersection of the asymptotes. Between b = -2 and b = 10, the graph lies in the first and third quadrants of the intersection of the asymptotes. Thus we can see that the parameter b changes the point that the graph cuts the y-axis, by the amount equal to the letter b.and the graph narrower and narrower as it goes towards the the point y=-2, and wider and wider as it goes away from the point y = -2.
Changing the parameter c

The results of the observation after the changing of c is as follows:
1) The y-intercept for all the graphs is at y = -1.Recall that the y-intercept is the value of y when x = 0. since when x=0, the value of cx = 0, thus changes in c this will have no effect on the y- intercept. The y-intercept is the point (0, b/d).
2) The x-intercept for all the graphs is at x = -1/2.Recall that the x-intercept is the value of x when y = 0. The x-intercept is the point (-b/a, 0). Changes in c do not cause changes in the x-intercept.
3) All the graphs, except the ones in which c = 0 and c = -2, are hyperbolas, therefore at c = 0 and c = -2, there is a special case for the rational equation.
4) The graphs of the hyperbolas all have different vertical asymptotes which vary according to the value of c. When c = 10, the vertical asymptote is at x = 0.1, while when c = -5, the vertical asymptote is at x = 0.4. Thus one might be want to deduce that the value of the vertical is the inverse of the value of c. But recall that the vertical asymptote occurs where the denominator equals zero, so because the value of d is -1, then setting cx + d = 0, will result in the vertical asymptote occurring at the inverse if the value of c.
5) The graphs of the hyperbolas have different the horizontal asymptotes for the changing values of c, are equivalent to the value of a/c at each point.
6) As we move from left to right along the graph we notice that the graphs flip as you move past the vertical asymptote. The light blue graph is always an increasing function, while the purple and red functions are always decreasing functions. Notice that for the light blue hyperbola ad - bc > 0 and for the purple and red curves ad and bc < 0.
In order to observe what happens when the graph changes in dynamic form, we then let c take on values from 10 to -10. Observe the graph changes and record what happens.
Notice how the changes in the value of c changes the graph. When the value of c = 1, there vertical asymptote is 1, when c = 2, the vertical asymptote is 0.5, when c= 4, the vertical asymptote is 0.25. Notice here that the vertical asymptote is the inverse of the value of c. Notice that as c becomes larger and larger, the vertical asymptote gets closer and closer to x = 0, but never touches 0.
Changing the parameter d.
Holding the parameters a, b, and c constant, the parameter d is now changed according to the values d = 5, 2, 0, -2, and -5. The diagram below shows what happens as d takes on the values shown.

The results of the observation after the changing of d are as follows:
1) The y-intercept for the graphs change as d is changed. When d = 5, the y-intercept is 1/5 and when d = -2, the y-intercept is -1/2. Changes in d affects the y-intercept because the y-intercept occurs at the point (0, b/d).
2) The x-intercept for all the graphs is at x = -1/2. The x-intercept is the point (-b/a, 0). Changes in d do not cause changes in the x-intercept.
3) All the graphs for the chosen values of d are hyperbolas.
4) The graphs of the hyperbolas all have different vertical asymptotes which vary according to the value of d. When d = 5, the vertical asymptote is at x = -5, while when d = -2, the vertical asymptote is at x = 2. Thus one might be want to deduce that the value of the vertical is the negative of the value of d. But recall that the vertical asymptote occurs where the denominator equals zero, so because the value of d is -2, then setting cx + d = 0, will result in the vertical asymptote occurring at the negative if the value of d.
5) The graphs of the hyperbolas have the same horizontal asymptote at y = 2.
6) As we move from left to right along the graph we notice that the graphs flip as you move past the vertical asymptote. In this case, the purple and red graphs are always an increasing functions, while the light blue, green and dark blue functions are always decreasing functions. Notice that for the purple and red hyperbolas, ad - bc > 0 and for the light blue, green and dark blue curves ad and bc < 0.
In order to observe what happens when the graph changes in dynamic form, we then let d take on values from 10 to -10. Look at the movie below to see the changes that the graphs make as the value of d changes.
Some general observations about the investigation
1) The rational functions always tend to flip as you cross the vertical asymptotes but the functions are either always increasing or always decreasing depending on the difference between ad and bc, if ad - dc > 0, then the function is always increasing, If ad - bc < 0, then the function is always decreasing.
2) The horizontal asymptotes of the graphs occur at the value of a/c.
3) The vertical asymptotes of the graphs occur at the value of the denominator cx + d = 0.
4) there may be some special or degenerate cases where the rational functions are not hyperbolas but become straight lines.
5) The x-intercepts occur at the point (-b/a, 0)
6) The y-intercepts occur at the point (0, b/d)
So far we have investigated how the graph changes as the coefficients and constants of the rational; equation changes. We will take a look at some more cases where the degree of the numerator and denominator change.
Other rational functions.
 is the form of a rational function.
is the form of a rational function.
In all our investigations so far the degree of the numerator f(x) and the degree of the denominator g(x) were the same. The numerator and denominator of the rational equation were both of degree 1. When the numerator and denominator are both of degree one notice the vertical asymptotes exist and the vertical asymptotes occur at the point a/c.
The numerator is smaller than the denominator.
If in the equation  , f(x) < g(x), then a very interesting result occurs in the horizontal asymptote as shown in the following diagrams:
, f(x) < g(x), then a very interesting result occurs in the horizontal asymptote as shown in the following diagrams:
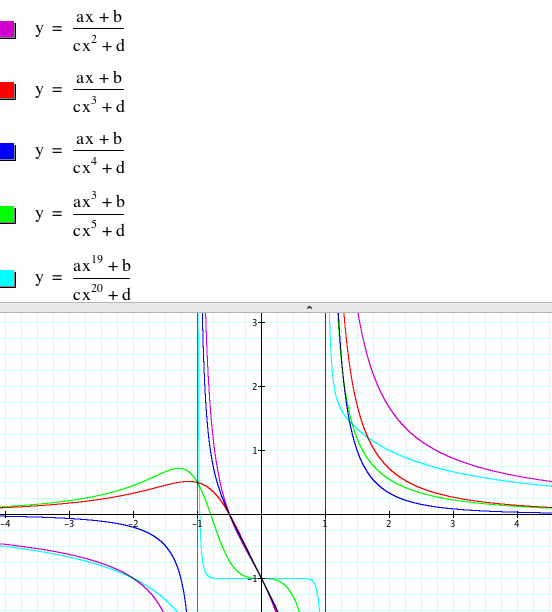
Notice that in all these diagrams the curves get closer and closer to the line y = 0, but never touch the line y = 0. Therefore, in the case where the degree of the numerator is smaller than the degree of the denominator, the horizontal asymptote is the x-axis.
Thus is further illustrated by clicking the movie link.
The numerator is larger than the denominator
If in the equation  , f(x) > g(x), then the result would look as shown in the following diagrams:
, f(x) > g(x), then the result would look as shown in the following diagrams:
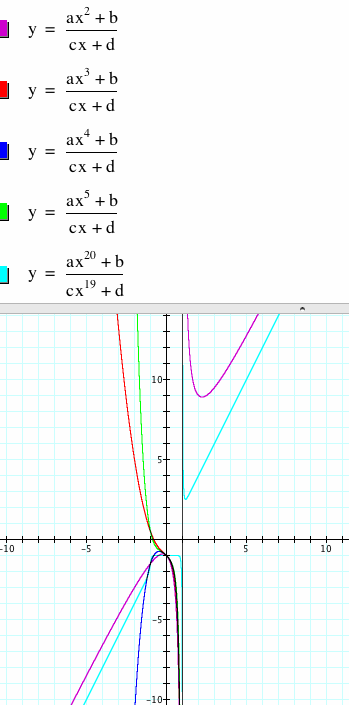
Notice what happens as the values get increasingly larger (in absolute terms). As the values of x get increasingly larger(in absolute terms) the values of y also get increasingly large (in absolute terms), so there is no horizontal asymptote.
Summary:
Given a rational function  :
:
1) The horizontal asymptotes of the graphs occur at y = a/c if the degree of f(x) is the same as the degree of g(x).
The horizontal asymptote is y = 0 when the degree of f(x) < degree of g(x).
The horizontal asymptote does not exist when the degree of f(x) > degree of g(x).
For the rational function of the form 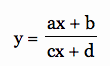 :
:
2) Rational functions are either increasing or decreasing depending on the difference between ad and bc, if ad - dc > 0, then the function is increasing; if ad - bc < 0, then the function is decreasing.
3) The vertical asymptotes of the graphs occur at the value of the denominator cx + d = 0. That is x = -d/c
4) There may be some special cases where the graphs of the rational functions are not hyperbolas but become straight lines. This can be explored in greater detail by the reader.
5) The x-intercepts occur at the point (-b/a, 0)
6) The y-intercepts occur at the point (0, b/d)
7) The hyperbola f0rmed is a rectangular hyperbola.


 , where f(x) and g(x) are polynomials and g(x) is not zero.
, where f(x) and g(x) are polynomials and g(x) is not zero.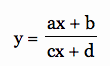

 where f(x) = ax + b and g(x) = cx + d, the horizontal asymptotes occur where the domain of the function breaks, that is where the denominator g(x) is equal to zero. In this case cx + d = 0, thus the vertical asymptote is x = -d/c. The horizontal asymptotes occur where y = a/c because as x gets infinitely large or small then the numerator tends to something extremely large times a or something extremely small times a, while the denominator tends to something extremely large times c or something extremely small times c.
where f(x) = ax + b and g(x) = cx + d, the horizontal asymptotes occur where the domain of the function breaks, that is where the denominator g(x) is equal to zero. In this case cx + d = 0, thus the vertical asymptote is x = -d/c. The horizontal asymptotes occur where y = a/c because as x gets infinitely large or small then the numerator tends to something extremely large times a or something extremely small times a, while the denominator tends to something extremely large times c or something extremely small times c.



 is the form of a rational function.
is the form of a rational function.  , f(x) < g(x), then a very interesting result occurs in the horizontal asymptote as shown in the following diagrams:
, f(x) < g(x), then a very interesting result occurs in the horizontal asymptote as shown in the following diagrams:
 , f(x) > g(x), then the result would look as shown in the following diagrams:
, f(x) > g(x), then the result would look as shown in the following diagrams:
 :
: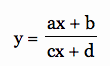 :
: