QUADRATIC FUNCTIONS Investigation
By Leighton McIntyre
Goal :
Assignment 2: To show what happens to the shape and position of the graph of a quadratic function when the a is varied and the significance of the graph when a = 0.
Given the quadratic function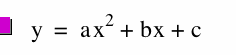 
where b = 1 and c = 2, we can choose different values of a to show what happens to the graph as a varies, THe values of a chosen are 4, 3, 2, 1, 0, -1, -2, -3, and -4. Observe what happens to the shape of the quadratic function in the diagram below:
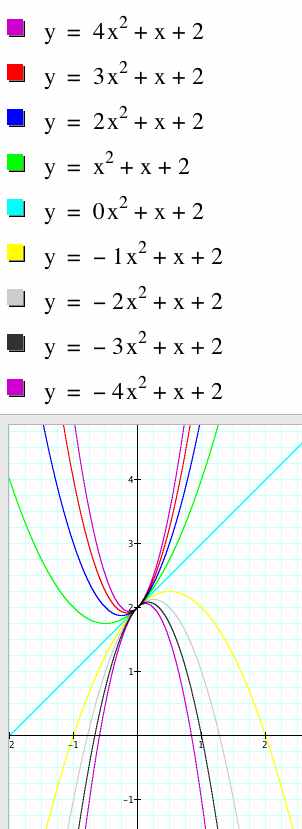
At the a = 4 the parabola opens upwards. As the constant a is varied the from 4 to -4, the graph of the function
gets wider and wider then becomes flatter and flatter until it is a straight line at a = 0. This is because when a = 0, the quadratic equation becomes a linear function. After the point a = 0, the parabola curves downwards and becomes narrower and narrower as the curve endpoints move toward the y axis. The mathematics behind all this is that the shape of the parabola is determined by the size and the sign of the constant a. The point where the parabola cuts the y-axis is determined by the shift factor, which in this case is 2. Notice that all the curves pass through the point y = 2. The movie of the quadratic function is shown below:
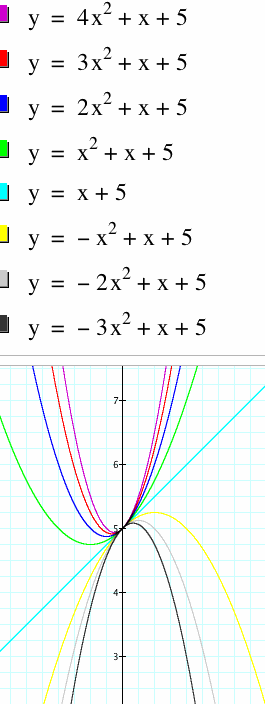
This function is then tested with other values of c, like c=-1 and c = 5
In the graph to the left below, the values of a range from 4 to -4, while the value of c remains at -1. Notice here that the parabolas of all the functions all pass through the point y = -1. In the graph to the right below, the values of a range from 4 to -3, while the c value is held constant at 5. The paraolas of all the functions pass through the point y = 5. Notice also that as the value of a changes from positive to negative, the shape of the parabola goes from upward curving to flat to downward curving.
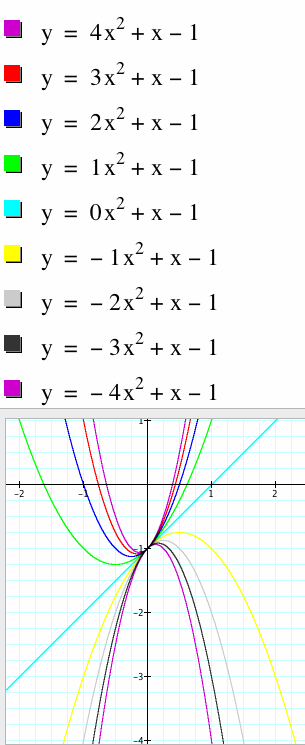
Summary
1) The a determines the curve of the parabola (how wide the parabola is).
2) The c determines the value that the parabola cuts through the y-axis.