By Leighton McIntyre
Goal : To examine the roots of the quadratic equation in the xb plane
Assignment 3
The basic structure of graphs in the xb plane relates graphs of the functional form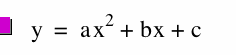 
form or the standard form 
to the form 
where the y in the second equation represents the b for graphing purposes.
Consider the equation 
The graph of this equation in the xb plane look like this:
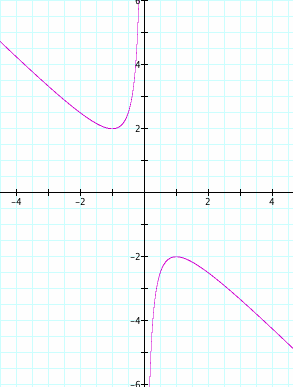
Given a value of b such as b = 5, we let y = 5 in the above case and we now have a graph that looks like this:
Notice the line crosses the curve at two points and so it has two roots.
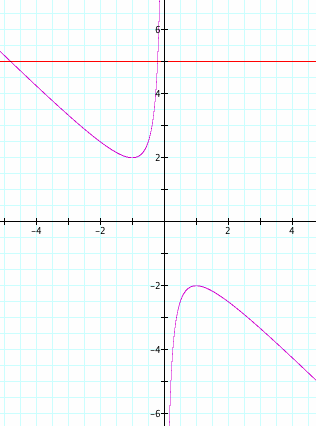
If we let b
= 4 the graph looks like this: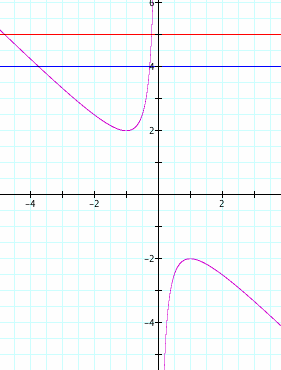 
Notice that, again the line crosses the curve at two points and thus has two roots.
If we set b = 2, the graph now looks like this: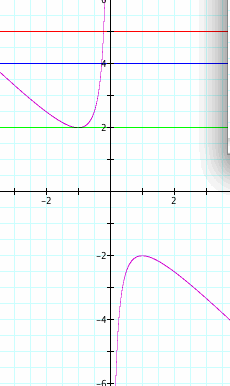
Here the line touches at only one point and thus at b = 2 there is only one root.
If we continue below b = 2 to b = 1 we find that the graph now looks like this: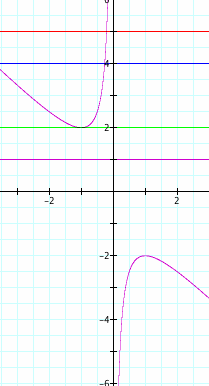 
Notice here that the line does not cross the curve at all and so at b =1 there are no roots. If we follow this pattern moving down the line we will notice one root again at b = -2 and two roots at b points less than -2.
Now let us investigate the case where the value of c changes from 1 to -1 in the equation. We now have a graph that looks like the one below. With the two original graphs imposed together we notice that the blue line at b = 5, if shifted up or down will cross the new equation graph at two places every time.
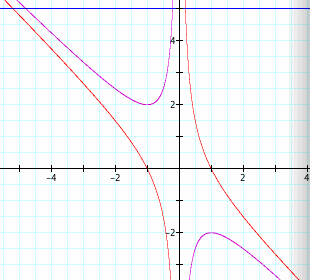
We show the following cases for our investigation and show what happens to the graph.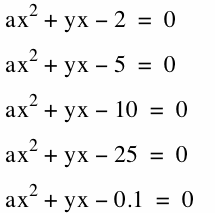
The graph of these equations is as follows: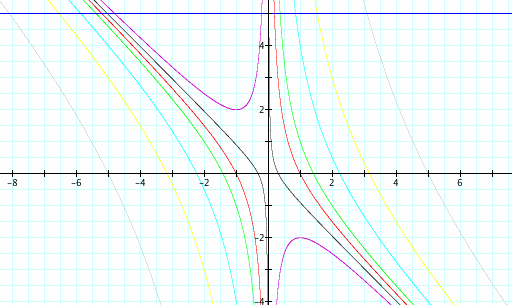
Now notice that as the absolute value of c goes from -2 to negative -25, the curve moves further and further from the origin but the basic shape stays the same; so that if we were to move the blue horizontal line up and down the graph, there would still be two places that the blue line would cross the curve. Even at the point where c = 0.01, there are still two points where the blue line would cross the curve. We can safely assume that for our investigation that whenever c < 0, then the graph will have two roots.
Let us view a movie of the way that shows this:
Summary
From the investigation we note that
1. The x values of the horizontal line that represent the value of b are the roots of the . The graph is a hyperbola and the horizontal line cuts the graph at two points, one point, on no point.
2. When c =1, is there will be one root at b = 2 and one root at b = -2. There will be no roots at -2 < b < 2, and two roots at
b > 2 and b < -2. All of the equations in this investigation occurred at a = 1.
3. When c = - 1. there will be two roots at all values of b.
4. The graphs of appear to be hyperbolas with the vertical asymptotes at x = 0, and the other asymptote at b = x
5. When c = 0, the hyperbolas collapse to the lines x = b and x = 0, which are the roots of the equations.
6. When c > 0, such as where c = 1, there is always a region with 2 roots, two points where there is one root and a region with zero roots. When b > 0, as b gets larger the roots are negative with one approaching zero and the other approaching -b. When b < 0, as the absolute value of b increases, the roots are positive with one approaching zero and the other approaching -b.
7. When c < 0, there are always two roots. One roots is positive and the other is negative. When b < 0, as b gets larger in absolute value, the positive root tends to -b and the negative root tends to 0. When b > 0, as b gets larger, the positive root tends to 0 and the negative root tends to -b.
Return to Leighton's Homepage.