

PEDAL TRIANGLE INVESTIGATIONS
By Leighton McIntyre
Goal : To investigate the behavior of pedal triangles of the different centers of a triangle, namely; the median, the incenter, the orthocenter and the circumcenter.
Pedal Triangle Construction
A pedal triangle can be constructed in Geometers Sketchpad (GSP) by first constructing a triangle ABC and then choosing an arbitrary point P in the plane of triangle ABC.
The process continues by extending the lines AB, AC, and BC, to which perpendicular lines are constructed from the point P.
The intersections of the perpendiculars from the point P with the extensions of the line segments AB, AC and BC, are labeled points DEF.
From these points construct segments to form triangle DEF, which is the pedal triangle to triangle ABC, with the pedal point P. See figure below.
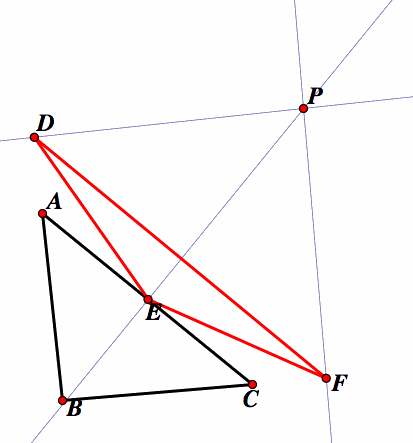
When the pedal point P is the centroid G.
The centroid of a triangle lies on the inside of the triangle and is the intersection of the three medians if the triangle. Our conjecture is that when P is the centroid the pedal triangle will always lies on the inside of the original triangle. The pedal triangle is constructed from the centroid and then animated to give different representations.
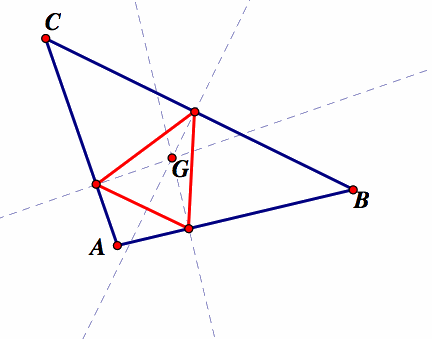
Note that G is the pedal point of the triangle. The red pedal triangle remains on the inside of the original triangle, regardless of whether the original triangle is acute, right, or obtuse. To further explore this in GSP click here.
When the pedal point P is the incenter I.
The incenter is the intersection of the three angle bisectors of the circle. Again, our conjecture is that the pedal triangle of the incenter being the pedal point will always be inside of the original triangle. The pedal triangle is constructed from the incenter and then animated to give different representations.
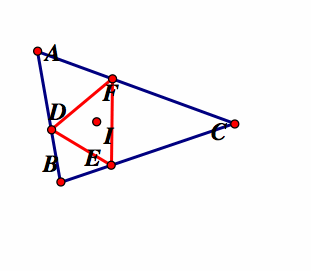
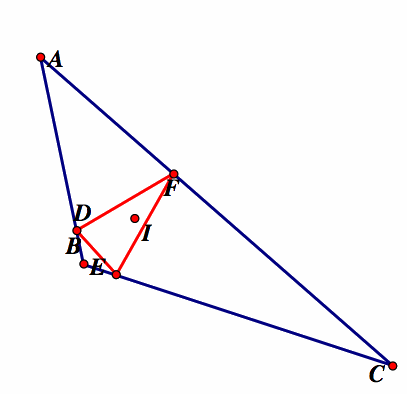
Note that G is the pedal point of the triangle. As our investigations show, the red pedal triangle remains on the inside of the original triangle, regardless of whether the original triangle is acute, obtuse, or right. To further explore this in GSP click here.
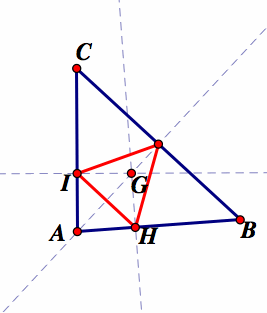
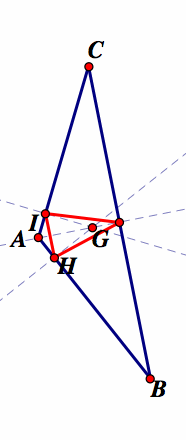
When the pedal point P is the orthocenter H.
The orthocenter of a triangle is the point of concurrency of the three perpendicular lines form the vertices to the opposite sides of the triangle. The orthocenter does not always lie inside the triangle. It may lie outside as in the case of an obtuse triangle, on a vertex as in the case of the right triangle.
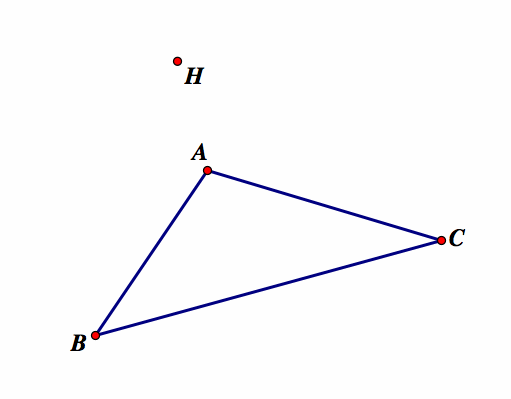
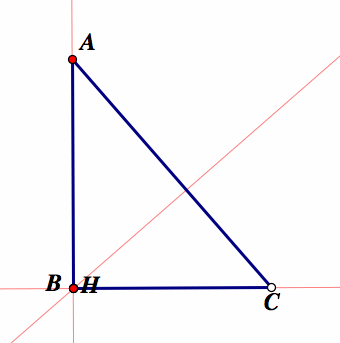
The pedal triangle is constructed from the orthocenter and then animated to give different representations.
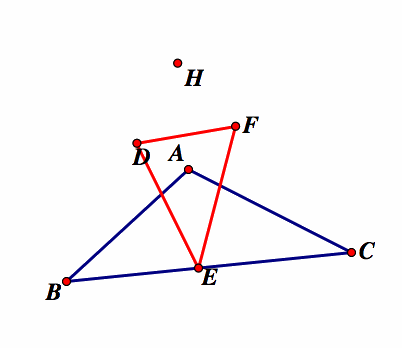
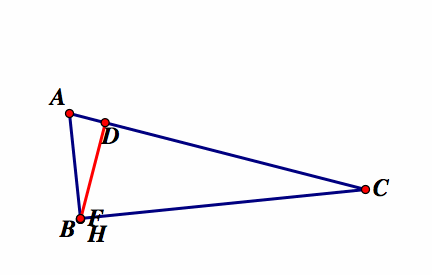

Note that H is the pedal point of the triangle. As our investigations show, one point of the red pedal triangle stays on one segment of the original triangle when the original triangle is obtuse. This is because one of the segments will be perpendicular to the pedal point through the angle bisector closest to the pedal point. The pedal triangle becomes a straight line when the original triangle is a right triangle. This is because the point of concurrency of the three perpendicular lines from the vertices to the opposite sides of the original triangles intersect at a vertex in the original triangle. The perpendicular from these segments become the pedal point at the vertex, so the only other perpendicular is to the segment opposite the right angle and thus the pedal triangle becomes a straight line. The pedal triangle remains inside inside of the original triangle when the original triangle is acute.
Further, from the definitions of the orthocenter, it follows that the when the pedal point is the orthocenter, the pedal triangle will be the orthic triangle.
To further explore this in GSP click here.
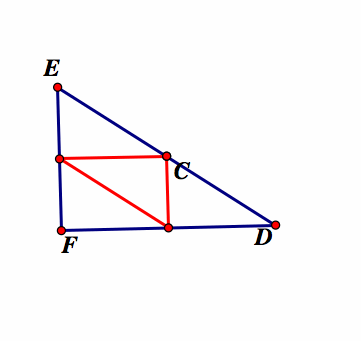
When the pedal point P is the circumcenter (C).
Circumcenter is the intersection of the three perpendicular bisectors of the triangle.
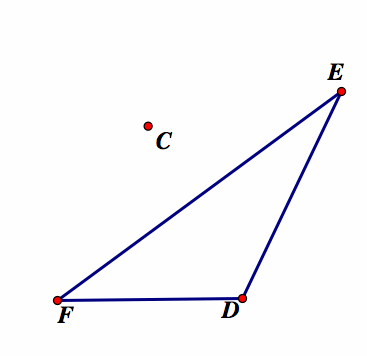
Note that the circumcenter (C) does not have to be outside the original triangle, but could be inside or even on one of the line segments. The pedal triangle is constructed from the circumcenter and then animated to give different representations. Our conjecture is that the pedal triangle will sometimes lie inside the original triangle and sometimes lie outside the original triangle. Because the orthocenter is constructed from the perpendicular bisectors of the sides of the triangle, the vertices of the pedal triangle will lie on the midpoints of the sides. The triangle that has vertices on the midpoint on another triangle is the medial triangle. This triangle always lies on the inside of the original triangle. Thus, the pedal triangle formed when the pedal point is the circumcenter will always lie inside the original triangle.
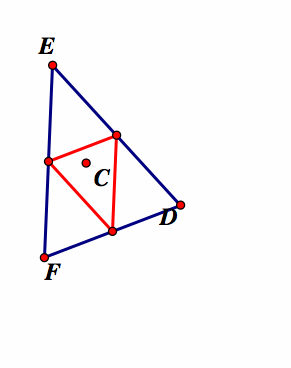
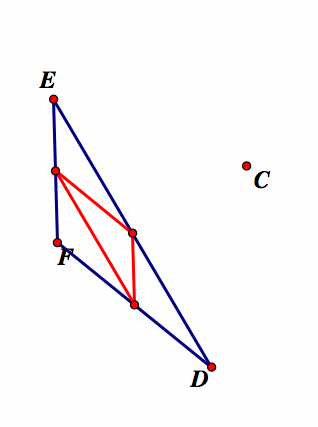

Summary
In our investigations we found something quite interesting. In all three situations, where the original triangle was acute, obtuse or right angled, the pedal triangle from the circumcenter always lie on the inside of the original triangle. See the red triangles above. How can this be explained? Recall that the circumcenter is the intersection of the three perpendicular bisectors of the triangle. Then if we construct a pedal triangle from the circumcenter, then we will have to find the intersection of the perpendicular from the circumcenter and the line segment to which it is perpendicular will always lie on the line segment. Therefore the vertices of the pedal triangle will lie on the line segments of the original triangle and this will cause the pedal triangle to always be inside of the original triangle. To further explore this in GSP click here.