
We will here first examine quadratic functions of the form
![]()
where a,b ∈ ℕ are fixed and c ∈ [-4,4].
We will consider g(x) = ax2 + bx + c as a function resulting from a transformation of f(x) = ax2 + bx. Any such function f(x) = ax2 + bx is a parabola with roots
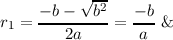
![]()
We can calculate the axis of symmetry by averaging the values of the roots:
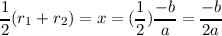
Now, let’s consideration the function g(x) = ax2 + bx + c. We know that the mapping f(x) f(x) + c is a vertical translation of f(x) by c units (upward if c > 0, downward if c < 0).
f(x) + c is a vertical translation of f(x) by c units (upward if c > 0, downward if c < 0).
Intuitively, f(x) and g(x) should have the same axis of symmetry. We can check as follows. The
roots of g(x) are:
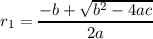
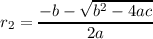
Averaging the two to get the axis of symmetry,
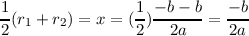
Indeed, f and g have the same axis of symmetry, x = 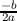 .
.
Therefore, f and g are parabolas with the same shape, but g is a vertical shift of f by c units.
The following is an animation of this translation as c ranges within [-4,4].
Now, let us also consider the function
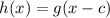
In
this form, it is apparent that h is horizontal translation of f by c units (if c > 0, the translation
is horizontally in the positive direction; c < 0 and the translation is in the negative
direction).
Let us now expand h(x).
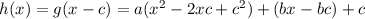
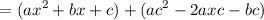
We
could have expected that h would have a more complex constant term, as well as a different
factor of x (as compared to g(x)).
How does h move as c changes within [-4,4], though? As it is both a vertical translation of c and
a horizontal translation of c of g(x), we know that the function - in particular its vertex - should
travel along a line with slope  = -1.
= -1.
In investigating this function, it was discovered that the particular line along which h(x) moves
as c increases and decreases is quite interesting, as it depends on a,b as opposed to c. We know
that the line y = mx + b0 which the translated function moves along as c ranges must
have a slope of m = 1. We can then rewrite the equation of this line as -x + y = b0.
We now need a point that any such line will travel through in order to determine its y-intercept..
Let us look at the vertex.
The axis of symmetry for h(x) will lie at the x-value that is the average of the values of the two
roots. Using the quadratic formula on
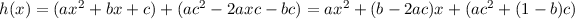
we get that
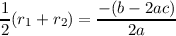
The
axis of symmetry of h(x) is thus x = 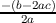 and the vertex is
and the vertex is
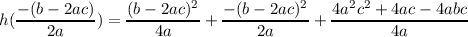
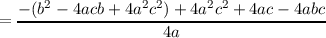
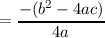
Therefore, the vertex of h(x) is (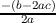 ,
,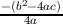 ), and we can solve for the y-intercept of our
line by calculating
), and we can solve for the y-intercept of our
line by calculating
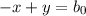
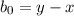
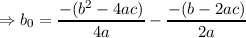
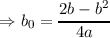
Therefore, given any quadratic g(x) = ax2 + bx + c with varying c, one can determine the line
along which the horizontal translation h(x) = g(x-c) solely from the coefficients. In particular,
this line is
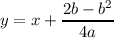
For an animation of the movement of h(x) along this line as c ranges from -4 to 4, see the following: (note: to pause or resume the video, click or double-click, respectively)