
Newton’s
Law of Cooling
An
Experimental Investigation
by
Elizabeth Gieseking
When an object is at a different
temperature than its surroundings, it will gradually cool down or heat up until
the temperatures are equal. Everyone has
experienced this. You boil water to make
tea and then wait several minutes until it is at a temperature at which you can
drink it. You place a cold turkey in the
hot oven for Thanksgiving dinner and after several hours it has reached the
desired temperature. Newton’s Law of
Cooling relates the rate of change in the temperature to the difference in
temperature between an object and its surroundings.
![]()
where ![]() the temperature of the object of interest as a
function of time
the temperature of the object of interest as a
function of time
![]() the time
the time
![]() the ambient temperature
the ambient temperature
![]() the
initial temperature
the
initial temperature
![]() a
proportionality constant specific to the object of interest
a
proportionality constant specific to the object of interest
This differential equation can be
integrated to produce the following equation.
![]()
Experimental Investigation
For this exploration, Newton’s Law of
Cooling was tested experimentally by measuring the temperature in three beakers
of water as they cooled from boiling.
The purpose of this investigation was twofold. First I wanted to determine how well Newton’s
law of cooling fit real data. Second, I
wanted to investigate the effect of changing the volume of water being cooled.
Three beakers of water were used for this
experiment. The first held 100 ml of
water, the second 300 ml, and the third 800 ml.
All three beakers originally held water at 100°C. Each beaker had its own thermometer and the
thermometers were kept in the beakers between measurements so there would be no
temperature lag. The temperature of the
water in each beaker was measured every minute, always in the same order. The ambient temperature for this
investigation was 23°C. The experimental
setup is shown below.

The temperature was measured
every minute for 35 minutes and then every 5 minutes for the remainder of one
hour. The following data was obtained.
|
Time (min) |
100 ml Temperature °C |
300 ml Temperature °C |
800 ml Temperature °C |
|
0 |
100 |
100 |
100 |
|
1 |
95 |
95 |
96 |
|
2 |
82 |
91 |
95 |
|
3 |
79 |
87 |
92 |
|
4 |
74 |
84 |
90 |
|
5 |
70 |
81 |
88 |
|
6 |
67 |
78 |
85 |
|
7 |
65 |
76 |
83 |
|
8 |
61 |
73 |
80 |
|
9 |
59 |
71 |
78 |
|
10 |
57 |
70 |
76 |
|
11 |
56 |
68 |
75 |
|
12 |
54 |
66 |
74 |
|
13 |
52 |
64 |
73 |
|
14 |
51 |
63 |
71 |
|
15 |
50 |
61 |
70 |
|
16 |
49 |
60 |
68 |
|
17 |
48 |
58 |
66 |
|
18 |
47 |
58 |
66 |
|
19 |
45 |
56 |
65 |
|
20 |
45 |
55 |
63 |
|
21 |
44 |
55 |
62 |
|
22 |
43 |
54 |
61 |
|
23 |
42 |
53 |
60 |
|
24 |
42 |
52 |
60 |
|
25 |
41 |
51 |
59 |
|
26 |
41 |
50 |
58 |
|
27 |
40 |
49 |
56 |
|
28 |
39 |
48 |
56 |
|
29 |
38 |
48 |
55 |
|
30 |
38 |
47 |
54 |
|
31 |
38 |
46 |
53 |
|
32 |
38 |
46 |
52 |
|
33 |
37 |
45 |
52 |
|
34 |
36 |
45 |
51 |
|
35 |
36 |
45 |
50 |
|
40 |
34 |
42 |
47 |
|
45 |
33 |
40 |
45 |
|
50 |
31 |
38 |
43 |
|
55 |
30 |
37 |
41 |
|
60 |
29 |
36 |
40 |
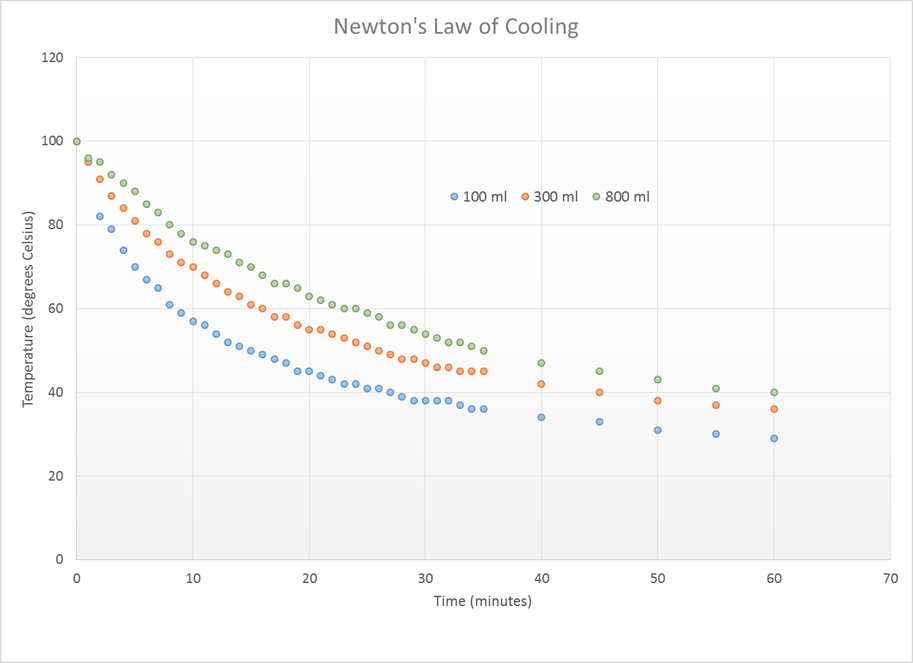
From this data, it can be
observed that the water in the smaller beakers cooled more quickly than the
water in the larger beakers. Below is a
graph of the data.
The next step is to determine the
value of k for each of the beakers of
water. We will look back at the
integrated equation and then solve for k.
![]()
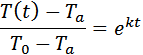
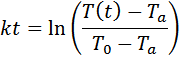
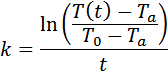
We will use Excel to calculate k at different times for each beaker and
then find the average k value for each beaker.
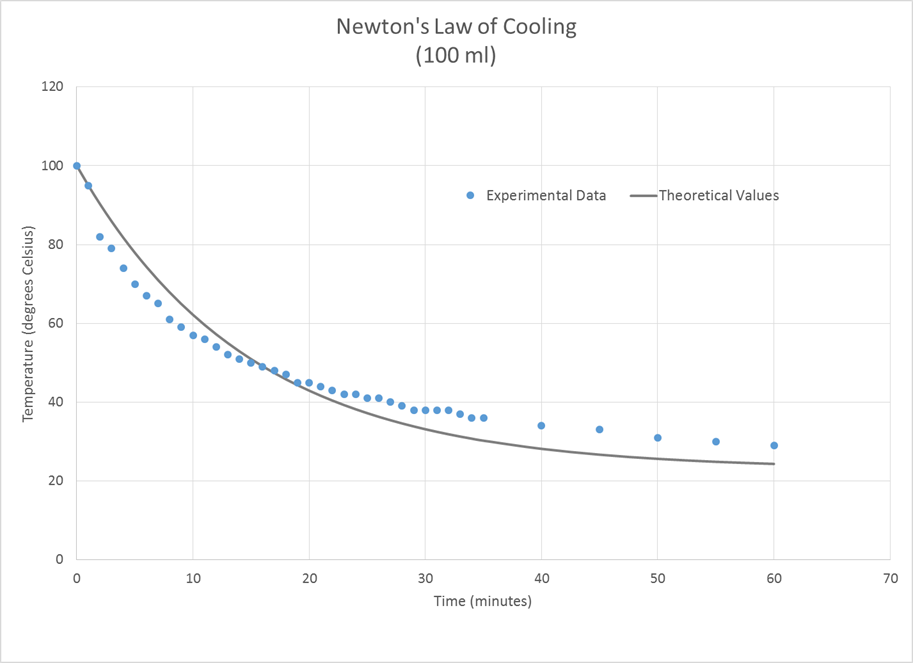
For the 100 ml sample of water, the
calculated k value was -0.0676. This resulted in a root mean square error of
4.80°.
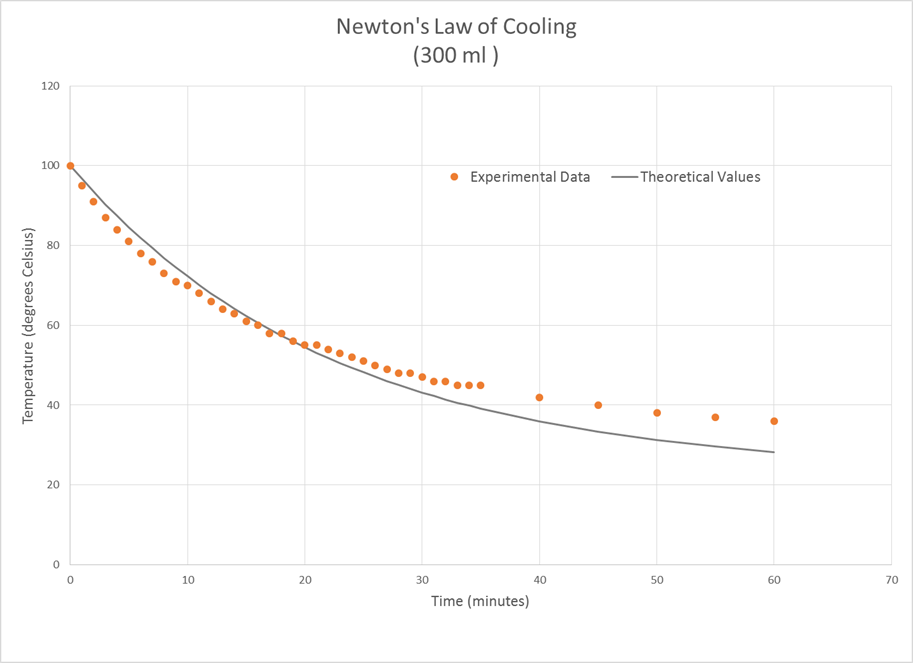
For the 300 ml sample, the calculated k value was -0.0447 and the root mean
square error was 3.71°.
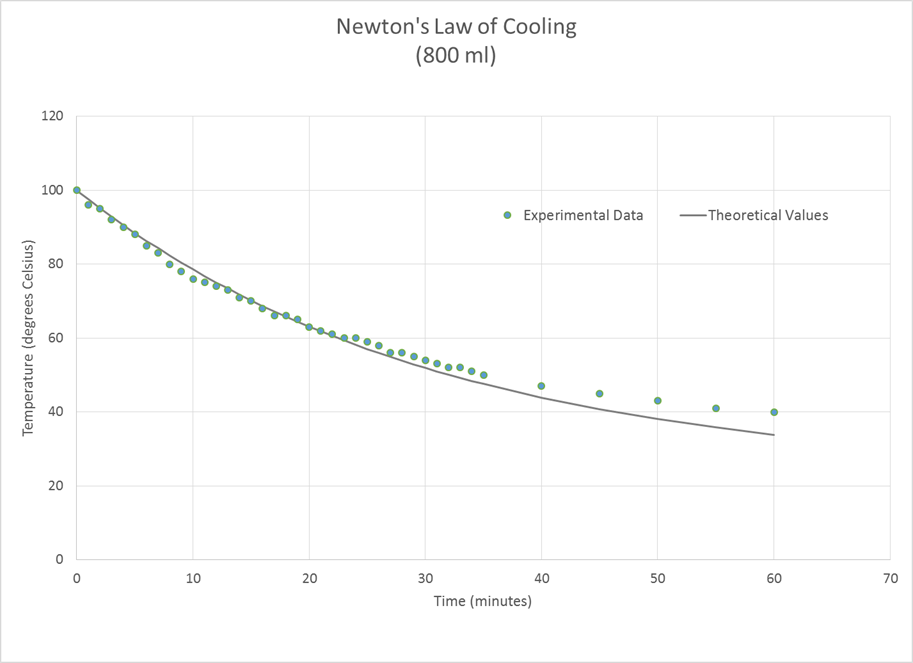
For the 800 ml sample, the calculated
value of k was -0.0327 and the root
mean square error was 2.24°. We note
that the value of k for the 800 ml
sample was about half of that for the 100 ml sample.
In
all of these cases, the experimental temperature fell more quickly at the
beginning of the experiment than that predicted by the theoretical model and
more slowly than predicted toward the end.
The larger water sample followed the Newton’s Law of Cooling model more
closely than the smaller samples did.
There are several explanations for this from a thermodynamics
standpoint. Newton’s Law of Cooling
accounts primarily for conductive heat exchange and assumes that the only heat
lost by the system to the surroundings is that due to the temperature
difference. At temperatures near
boiling, the rate of evaporation is high.
The heat lost through the phase change is greater than the heat lost
through convective heat exchange with the environment. Additionally, since the beakers were placed
on a granite countertop, the heat lost through conduction with the countertop
at the beginning of the experiment is significant and is higher than later on
when the countertop has warmed up. If
the countertop is now warmer than the surrounding air, the temperature gradient
is not what it was assumed to be from the initial temperature measurement. Despite these complications, we conclude that
Newton’s Law of Cooling provides a reasonable approximation of the change in
temperature for an object cooling in a constant ambient temperature.
Return to
Elizabeth’s Home Page