The Function of a Sine Curve and the Nature of its Parameters

by: Al Byrnes

Examine graphs of y = a sin(bx + c) for different values of a, b, and c.

Provide a mathematical interpretation of the Parameters a, b, and, c.

Explore using animations to illustrate the impact of each parameter.

Perhaps initailly not as intuitive as linear functions, understanding the effects of changing parameter values a, b, and c on the sine function y = a sin (bx + c) can be developed using programs such as Graphing Calculator or Desmos. The graph of the function y = sin x is shown below for reference.

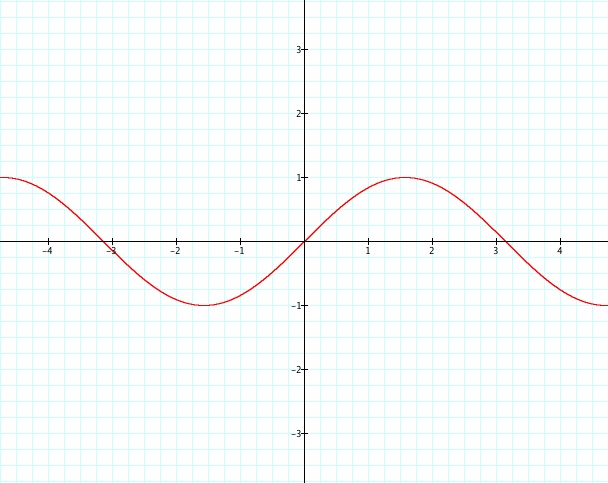
This visualization shows a sine curve with parameter values of a = 1, b = 1, and c = 0. What were to happen to the curve if we manipulated the values of each of the parameter values individually? Let's investigate for the curve y = a sin (bx + c)

Micro-investigation 1: Varying the value of parameter a; values of parameter b = 1 and parameter c = 0 held constant.

In this micro investigation we are interested in developing a mathematical interpretation of the effect of varying the value of parameter a on the curve y = a sin (bx + c). To this end we will examine several different values for parameter a in the sin function y = a sin x; below are illustrations of y = 1 sin x, y = 2 sin x, and y = 3 sin x, and y = 4 sin x

The distance from the x-axis to the peak of the trough seems to correspond to the value of the parameter a, eg: the peak of the trough of the sine curve is |a| from the x-axis. However, it is important to note that the points of intersection with the x-axis are not changed. This makes intuitive sense when some functions are set equal to zero and evaluated over the domain x = (0, π]

0 = sin(x) , x = π

0 = 2 • sin(x), x = π

0 = 3• sin(x), x = π

The point at which the value of the function y = a•sin(x) is zero is unaffected by the value of the parameter a. Therefore it we should not be suprized that multplication by a factor of a only affects the function when sin(x) does not equal 0.

Micro-investigation 2: Varying the value of parameter b; values of parameter a = 1 and parameter c = 0 held constant. Now let us investigate the effect on the shape of the sine curve when varying the value of parameter b. To get a base line for comparison, the function y = sin (x) is displayed below:

First, let's double the value of the parameter b, resulting in a new function: y = sin (2x); see the function graphed in the plane alone and in the second illustration with the functions y = sin (x) and y = sin (2x) graphed on the same plane:

... and now y = sin (x) and y = sin (2x) on the same graph:

What's happening here as we increase the value of the parameter b in the function y = sin (bx)? The y = sin(2x) curve appears to be squeezed together in such a way as half the wave period (note the value at which the y = sin(x) curve crosses the x-axis for the first time right of the origin appears to be approximately at x = 3.14, where the function y = sin(2x) seems to first cross the x-axis at a value half of the first intersection with the x-axis for the function y = sinx. Algebraically, this observation makes sense set y = 0 and compare the two equasions. Domain for x = (0, π]

0 = sin(x), x = π

0 = sin(2x), x = π/2, π

Lets try y = sin (3x):

... and compared to y = sin(x):

Here, we observe that the sine curve is "compressing" even more. This leads to another interesting algebraic connection. Set both functions y = sinx and y = sin3x equal to 0. Again, domain for x for this demonstration is x = (0, π]

0 = sin (x), x = π

0 = sin (3x), x = π/3, 2π/3, π

So as values of b continue to get larger, we can predict a corresponding "compression" of the sine curve, shortening of the wave period, and more solutions to the function y = sin(bx) over a given domain.

What might be a prediction for the effect on the sine function curve's shape if the parameter b is assigned values less that 1? My guess is a "stretch" of the curve, rather than the previously observed compression of the curve. The function y = sin(.5x) is shown below:

Now, y = sin (.5x) and y = sin(x) graphed in the same plane:

Indeed, our hunch seems to have been confirmed. The function's first intersection with the x-axis to the right of the origin is additionally where we might have expected it to be, a distance twice as far from the origin point. We can confirm this with algebra, by setting both y = sinx and y = sin.5x equal to 0 and considering possible solutions for the functions in the domainx = (0, 2π]:

0 = sinx, x = π and 2π

0 = sin x/2, x = 2π

Therefore, the parameter b can be interpreted as a compression or stretch, or in another way, a dialation of the sine curve by a factor of b.

Micro-investigation 3: Varying the value of parameter c; values of parameter a = 1 and parameter b = 1 held constant. For this micro investigation, we shift our attention to the final parameter of the sin function, c. For a basis of comparison, we should first take a look at the graph of the function y = sinx:

... and now the graph of y = sin(x + π/2) displayed along with the graph of y = sin(x + 0):

Note that the red sine curve, representitive of the function y = sin (x + π/2) seems to have "shifted" π/2 units to the left. What about y = sin (x + π)? y = sin (x + 3π/2)? y = sin (x + 2π)? How would these graphs of these functions look in the plane?

y = sinx and y = sin (x + π)

y = sin x and y = sin (x + 3π/2)

y = sin x and y = sin (x + 2π)

Note that with the final graph, the original function has just "shifted" or translated so far to the left that the function y = sin (x + 2π) (indicated in yellow) is sitting directly a top the function y = sinx. Alegbriacally, this translation makes sense as well: consider the functions y = sin x and y = sin (x + π/2), as shown in the graph below:

If evaluated at π, we will receive the following result:

y = sin (π) = 0

y = sin (π + π/2) = sin (3π/2) = -1

The addition of a positive parameter c should then be thought of as a translation of the curve -c units of the curve along the x-axis. Algebrically, this addition of c might also be thought of as a shift further along the unit circle; sin (x + c) an just be interpreted as the sine of the value of the angle x + a.

Return to top

Return to my student page