

In this exploration, we are going to construct a graph of any function y = f(x) by generating a table of values with the x values in one column and the y values in another. Then we will use a spreadsheet to display the graphs of parametric equations. Last, we will explore problems of growth.
First, we will start of generating a table
of values with the x values in one column and the y
values in another and construct a graph using Excel. In the first
example, we are going to construct the graph of ![]() .
Here is the table we will be graphing.
.
Here is the table we will be graphing.
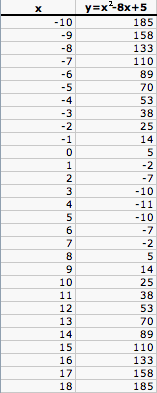
Let's now look at the graph of this in Excel.
We know that quadratic equations yield parabolas, so we should
get a parabola as the graph of ![]() .
.
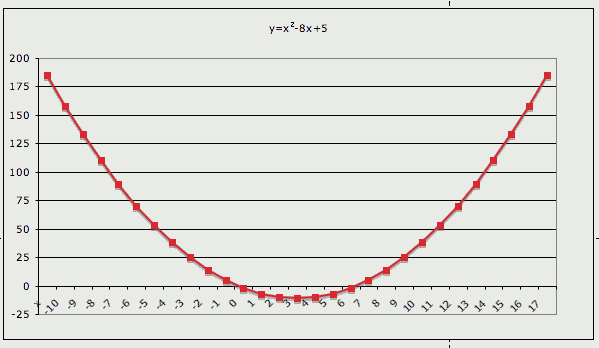
As we can see, the graph is a parabola. Now, we will construct a table involving parametric equations and see the graph using Excel. The parametric equations we will graph are x = 6 + t and y = 2 + 4t for -5 < t < 5.
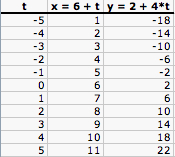
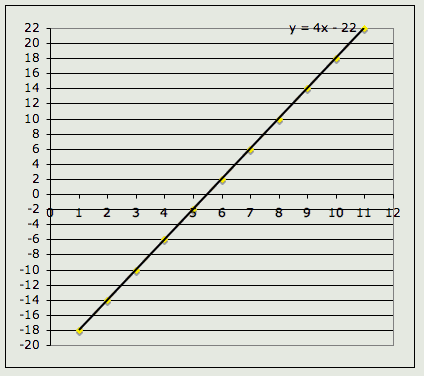
As we can see, the graph of these parametric equations is a line with a slope of 4. Finally, let's look at a table generated by the growth of a savings account. In the first example, we have an initial deposit of $10,000 made at the beginning of Year 1. The interest rate is 5% compounded annually. No deposits into the account are made during each year. Here is a table of the account balances over the next 30 years.
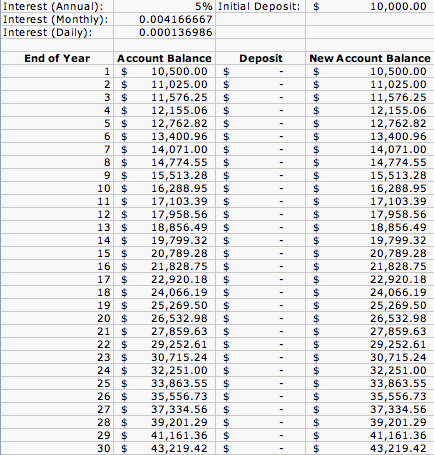
Now, let's look at the graph and see what the equation of the graph is.
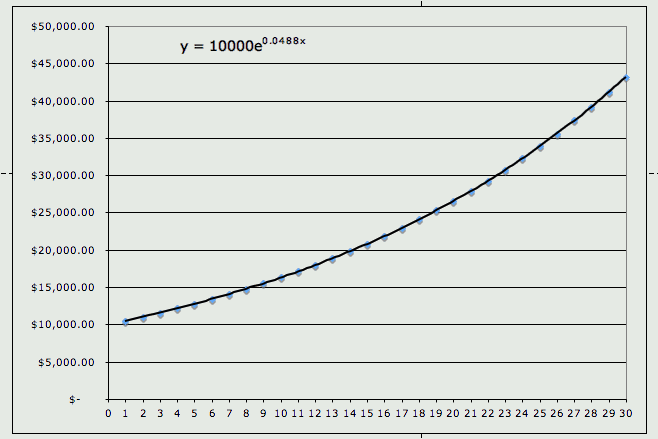
From this, we can predict how much will be in the account after 40 years. Plug in 40 for x and you should get y = $70,427.59. What happens if you deposit $1200 into the account at the beginning of every year ($100 per month)? Let's take a look at the table and graph.
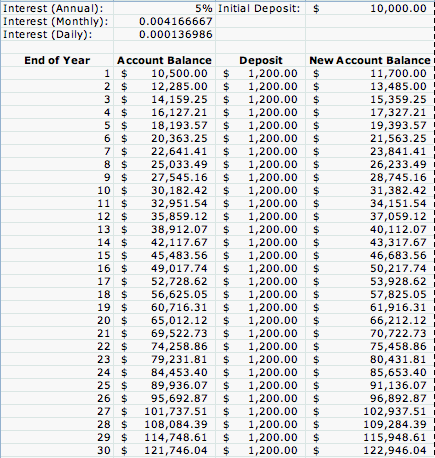
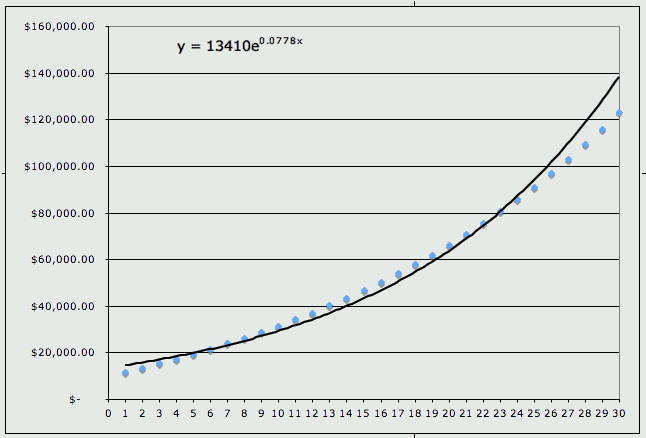
As you can see, the equation is not exact, but it gives a good prediction of what might happen if you deposit for 40 years. Depositing $1200 a year will give you more money after 30 years than if you didn't deposit anything and let the money grow for 40 years. What if the interest was compounded monthly instead of annually? Let's see the table and graph.
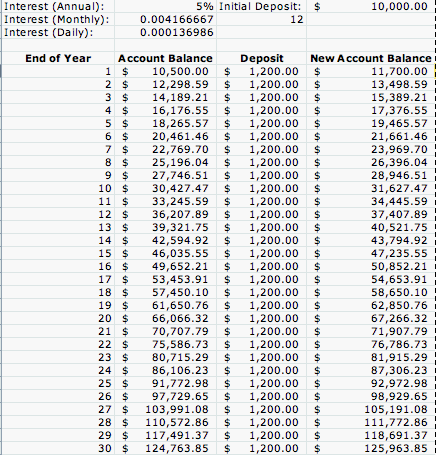
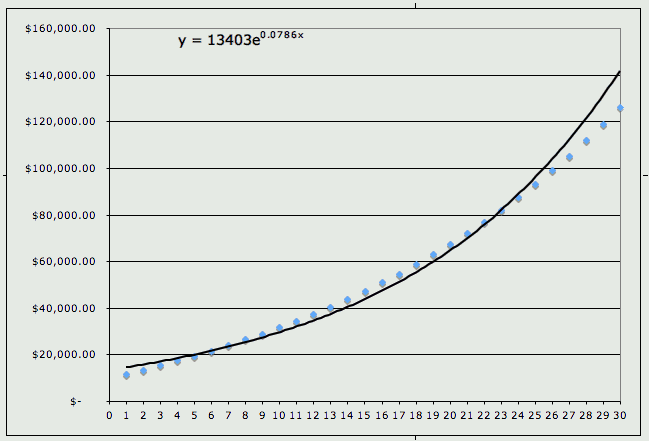
As you can see, compounding interest monthly will give you more money that compounding interest annually.
Click HERE to change the initial deposit, interest rate, annual deposit, or number of years. Make sure the update the formulas correctly!