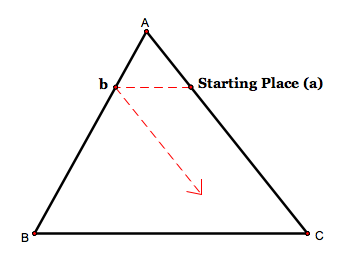
Final Exam: Bouncing Barney

Barney is in the triangular room shown here. He walks from a point on AC parallel to BC. When he reaches AB, he turns and walks parallel to AC. When he reaches BC, he turns and walks parallel to AB. Prove that Barney will eventually return to his starting point. How many times will Barney reach a wall before returning to his starting point? Explore and discuss for various starting points on line AC, including points exterior to segment AC. Discuss and prove any mathematical conjectures you find in the situation.

Questions to answer:

1. Will Barney always return to his starting point?

2. If so, will Barney always travel the same distance?

a. When Barney starts at any point.

b. When Barney starts at the midpoint.

c. When Barney starts at the trisection point.

3a. Does the path create a pattern of similar triangles?

3b. Where might his starting point be so that the path would create congruent triangles?

4. What if Barney started at a point inside the triangle?

5. Anything special about the path if he starts at the centroid?

Extension:

Construct a GSP image and explore.

Go Back to HOME